The answer is: #5#.
As you can see from this drawing:
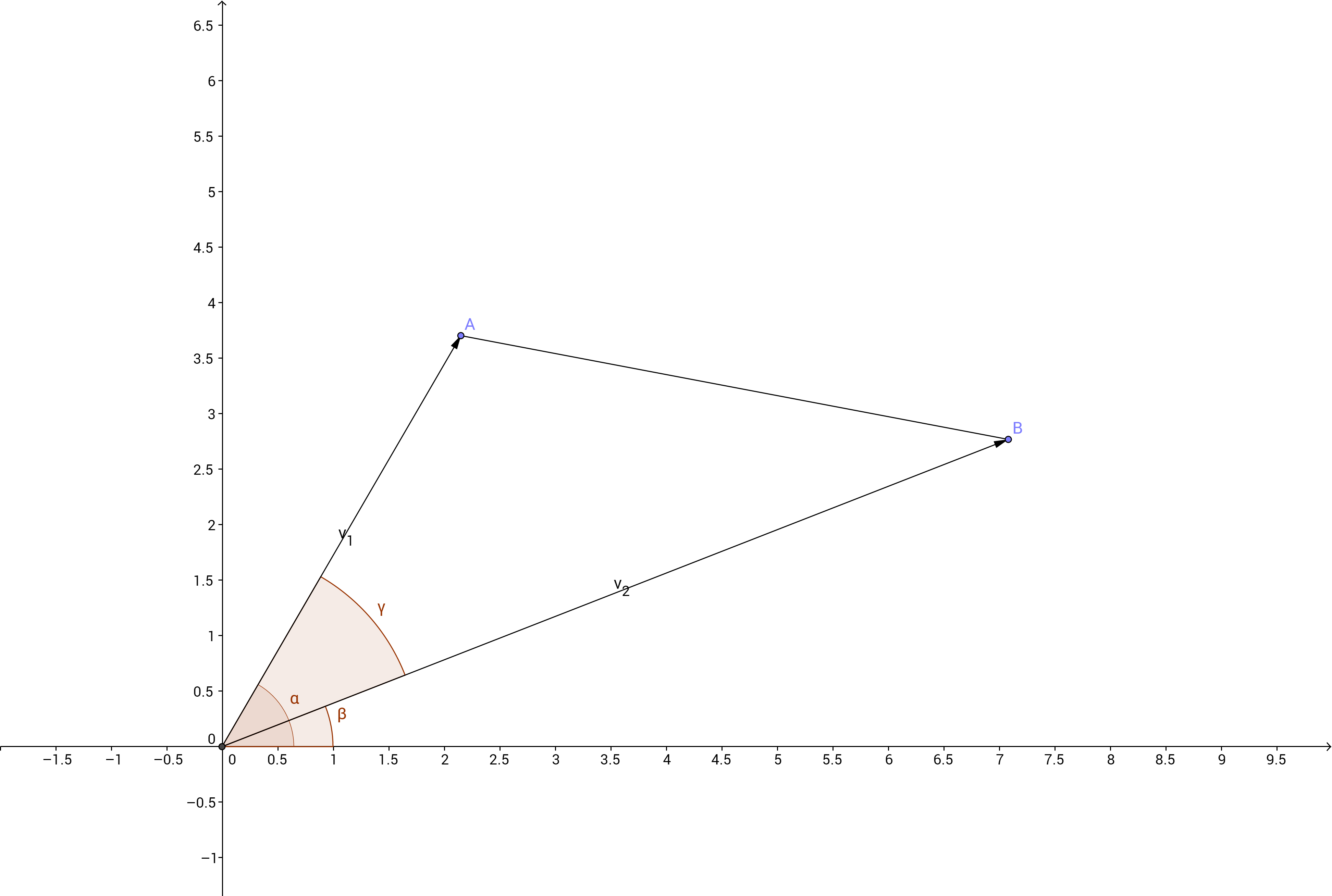
#A# and #B# in polar coordinates are #A(OA,alpha)# and #B(OB,beta)#.
I have named #gamma# the angle between the two vectors #v_1# and #v_2#, and, as you can easily see #gamma=alpha-beta#.
(It's not important if we do #alpha-beta# or #beta-alpha# because, at the end, we will calculate the cosine of #gamma# and #cosgamma=cos(-gamma)#).
We know, of the triangle #AOB#, two sides and the angle between them and we have to find the segment #AB#, that is the distance between #A# and #B#.
So we can use the cosine theorem, that says:
#a^2=b^2+c^2-2bc cosalpha#,
where #a,b,c# are the three sides of a triangle and #alpha# is the angle between #b# and #c#.
In our case:
#AB=sqrt(2^2+7^2-2*2*7*cos0°)=#
#=sqrt(4+49-28*1)=5#.
N.B.:
This is a very particular case, because the angle is the same for both the points (#10°#), so the two points are on the same line, and their distance could be easily calculate #AB=7-2=5#!


