You can consider an Eigenvalue as a scaling factor when you apply a matrix #A# to a vector #v# (which is a "special" vector called Eigenvector).
In mathematical terms: #A*v=lambda*v# (=the action of #A# on #v# is to SCALE of an amount #lambda# the length of #v#).
You can write:
#A*v-lambda*v=0#
#(A-lambdaI)v=0#
Where the identity matrix #I# was introduced to allow #v# to be factorized out and make possible the subtraction between matrices: #(A-lambdaI)#.
If you have a look at the expression #(A-lambdaI)v=0# you'll notice that it is simply the matrix equivalent of a system of homogeneous equations of the type:
#3x+2y=0#
#-2x-y=0#
This kind of systems may have a trivial solution (the origin, where all your lines cross) made up of all zeros or a non-trivial solution (an #oo# number of solutions, basically, all your lines are coincident). You want this last one (or at least one of the #oo# ones).
This non-trivial solution is obtained when:
#det(A-lambdaI)=0# (have a look at Cramer's Rule).
If you solve this equation for #lambda# you get all the possible Eigenvalues of your matrix #A#!!!
Let us see an example:
Consider a #2xx2# matrix #A#:
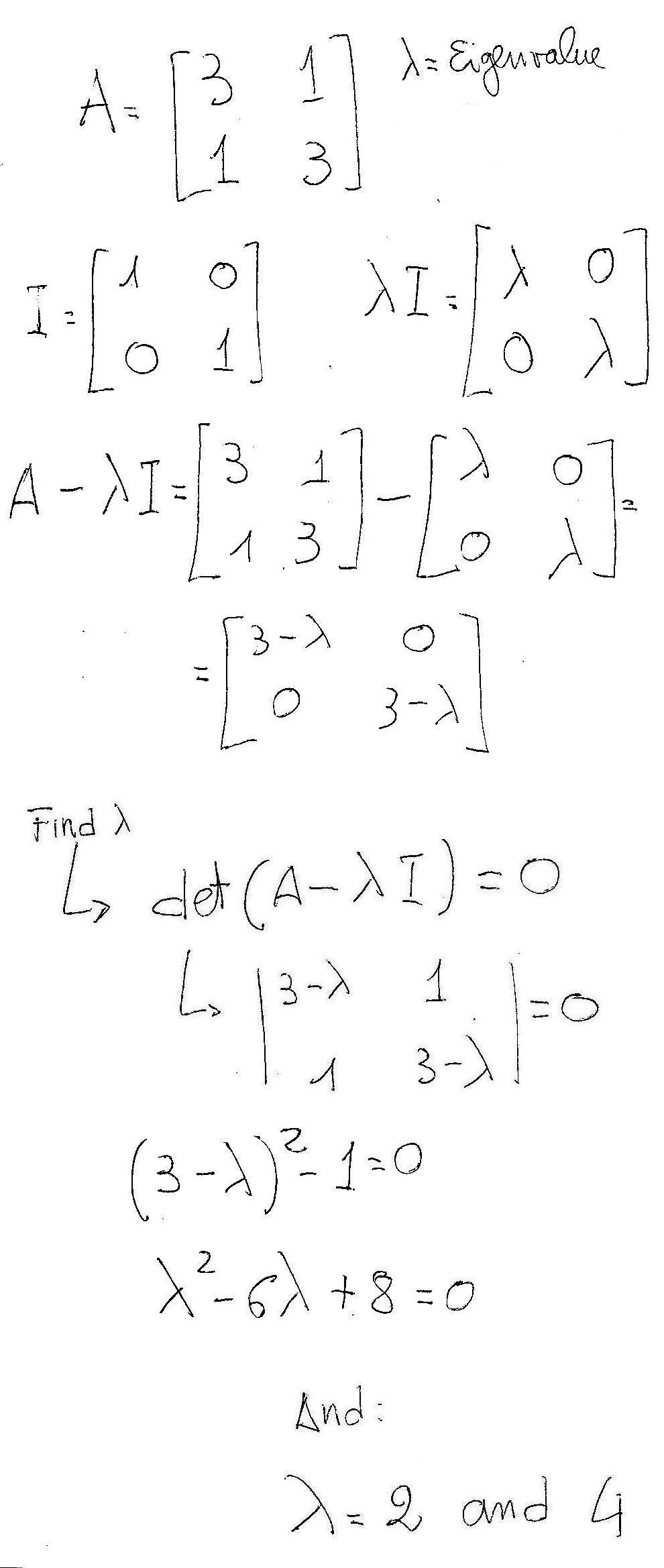
(hope it is not too confusing!!!)

