Elementary Row Operations
Key Questions
-
The transpose of a matrix is found by creating new matrix where the rows and columns are swapped out. If i denotes row and j denotes column, we have
#a_(ij)# becomes#a_(ji)# .Suppose you have a matrix A. The transpose is denoted
#A^T# . Let us take a 2 x 2 matrix for simplicity.#a_(11)# is row 1, column 1. The transposed entry would stay the in the same place.#a_(12)# is row 1, column 2. The transposed entry would be placed in Row 2, Column 1#a_(21)# .#a_(21)# is row 2, column 1. The transposed entry would be placed in Row 1, Column 2#a_(12)# .#a_(22)# is row 2, column 2. The transposed entry would stay in the same place.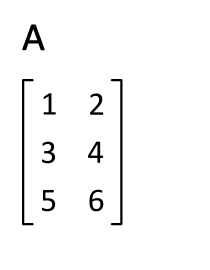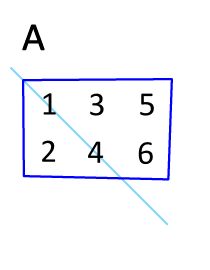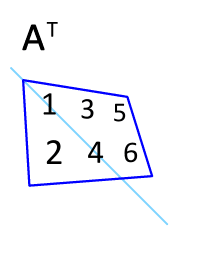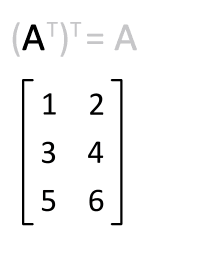
-
There are three elementary row operatins of matrices:
-
Exchange two rows position;
-
Substitute a row for the sum of it and another row;
-
Multiply a row for a scalar;
Hop it helps.
-