How do I find the #n#th power of a complex number?
1 Answer
You could use the complex number in rectangular form (
What you can do, instead, is to convert your complex number in POLAR form:
Graphically:
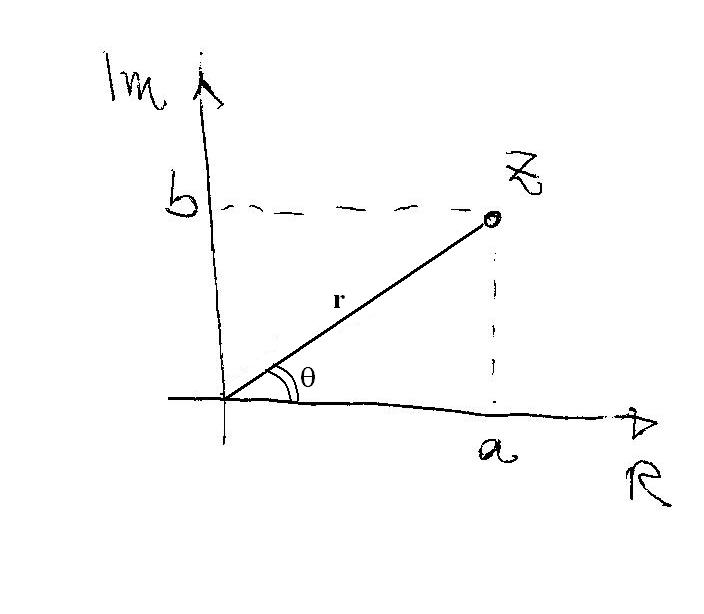
so that now the
Let's look at an example:
Suppose you want to evaluate
Using this notation you should evaluate:
But if you change it in polar form you get:
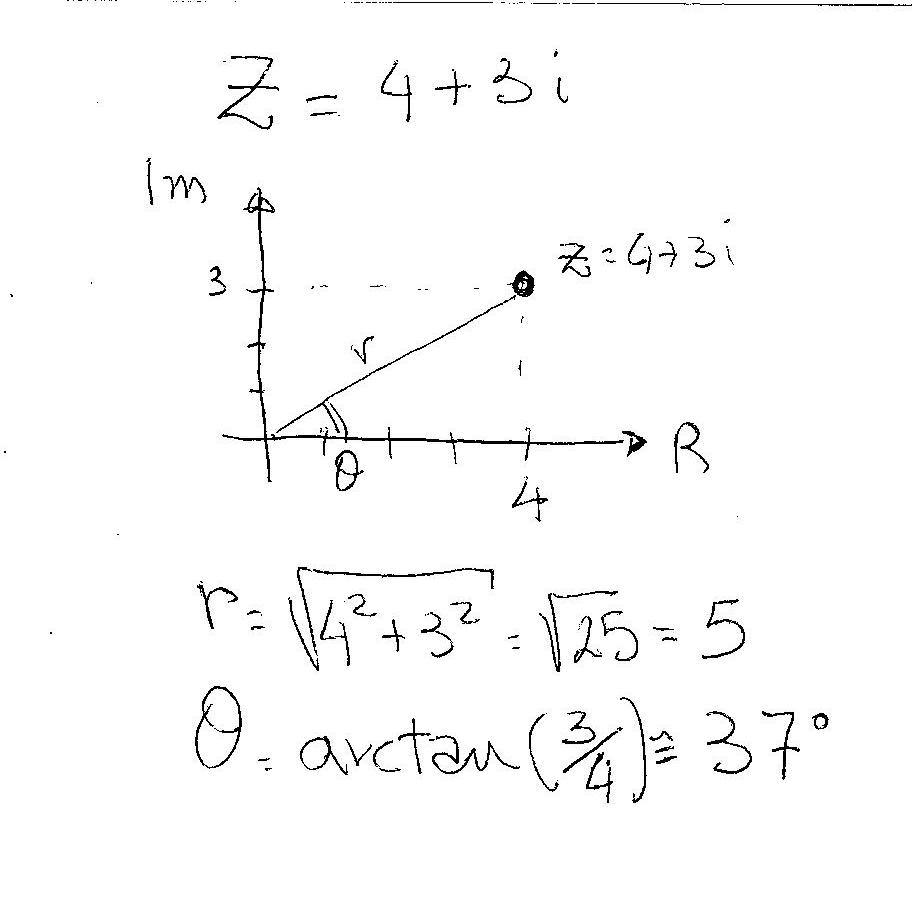
Your number in polar form becomes:
You can now wonder what is the rectangular form of your result.
We get there using the trigonometric form and do some math.
Looking at your
your complex number becomes now:
That gives you:
(I rounded a little bit to make it clearer)

