Powers of Complex Numbers
Key Questions
-
Given a complex number of form
#a + bi# ,it can be proved that any power of it will be of the form#c + di# .
For example,#(a+bi)^2 = (a^2-b^2) + 2abi# Knowing that, its less scary to try and find bigger powers, such as a cubic or fourth.
Whatsoever, any negative power of a complex number will look like this:
#(a+bi)^-n = 1/(a+bi)^n = 1/(c+di)#
This final form is not acceptable, as it has a division by#i# , but we can use a factoring method to make it better.
#(m+n)(m-n) = m^2-n^2# #-># #(m+ni)*(m-ni) = m^2+n^2# #1/(c+di)*((c-di))/((c-di)) = (c-di)/(c^2+d^2)# // -
You could use the complex number in rectangular form (
#z=a+bi# ) and multiply it#n^(th)# times by itself but this is not very practical in particular if#n>2# .
What you can do, instead, is to convert your complex number in POLAR form:#z=r angle theta# where#r# is the modulus and#theta# is the argument.
Graphically:
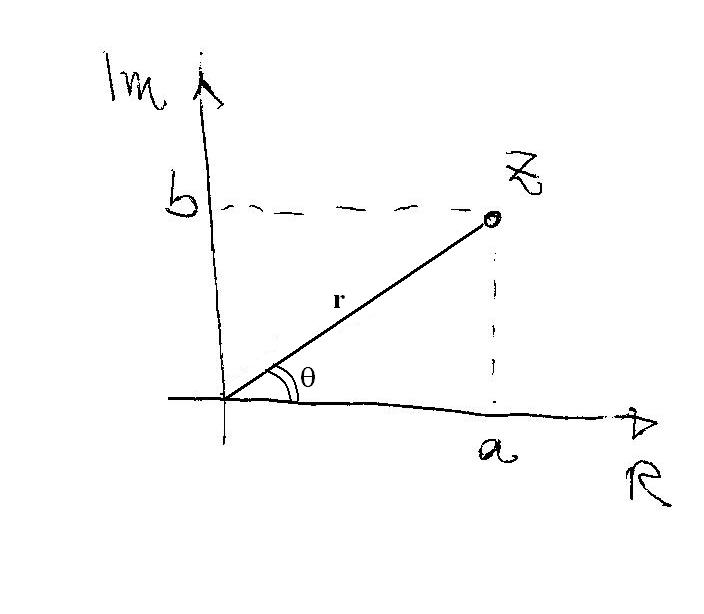
so that now the#n^(th)# power becomes:#z^n=r^n angle n*theta# Let's look at an example:
Suppose you want to evaluate#z^4# where#z=4+3i#
Using this notation you should evaluate:#(4+3i)^4# which is difficult and...well...boring!
But if you change it in polar form you get:
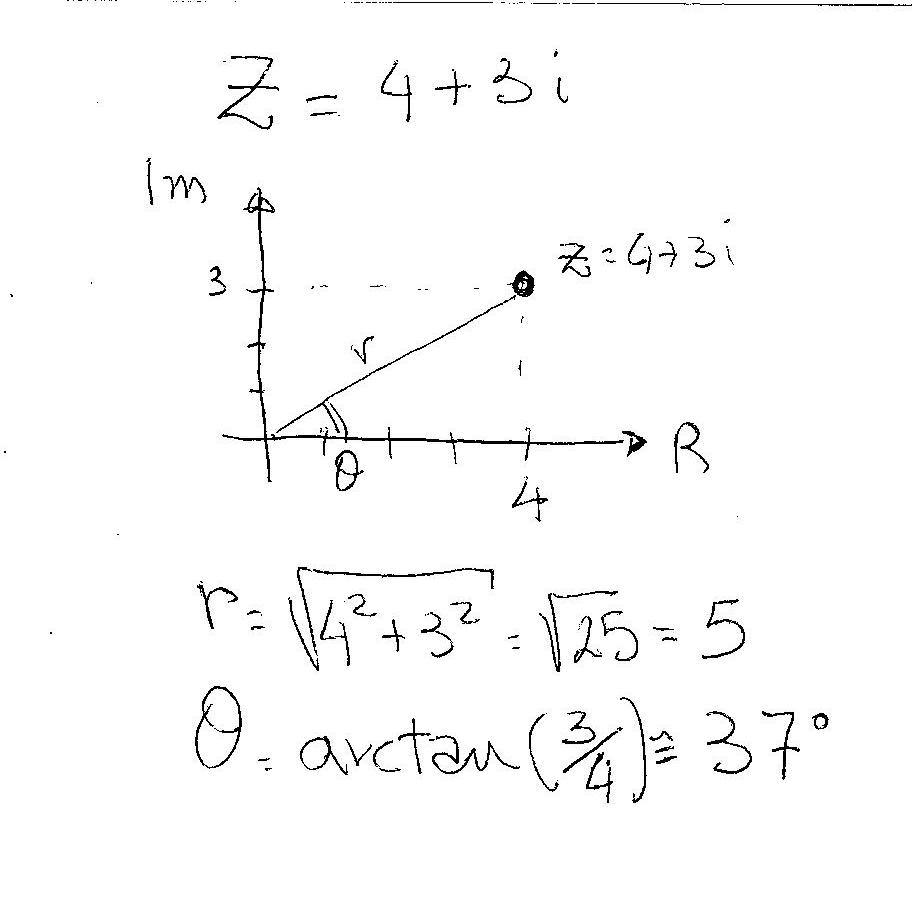
Your number in polar form becomes:
#z=5 angle 37°# and:
#z^4=5^4 angle (4*37°)=625 angle 148°# You can now wonder what is the rectangular form of your result.
We get there using the trigonometric form and do some math.
Looking at your#1^(st)# graph you can see that:
#a=r*cos(theta)#
#b=r*sin(theta)# your complex number becomes now:
#z=a+bi=r*cos(theta)+r*sin(theta)*i#
That gives you:
#z=-530+331i# (I rounded a little bit to make it clearer)
-
We can find the value of a power of i by using
#i^2=-1# .Let us look at some examples.
#i^5=i^2cdoti^2cdot i=(-1)cdot(-1)cdoti=i# #i^6=i^2cdoti^2cdoti^2=(-1)cdot(-1)cdot(-1)=-1# I hope that this was helpful.