How do I find the value of Cos 45?
3 Answers
It is
Explanation:
Well
Hence
Explanation:
Consider any right triangle with both its legs of same length. In this case both the other two angles would be 45 degrees each. Now, if both its legs are considered of unit length, then hypotenuse would be of length
The
Consider the idea that a triangle will always have an angle sum of
You may have seen that trigonometric functions are used directly on a triangles only when you have a right triangle. As in, when you "take the cosine" of an angle and do nothing else, the angle must be in a right triangle.
When you have that, you have:
Which means your three angles are
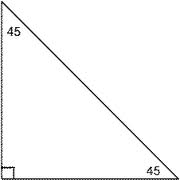
Let's say that you have a hypotenuse length of
You can convince yourself that if you draw a line from the bottom left corner of this triangle to the middle of the hypotenuse, you have drawn a line of symmetry and that these two legs are indeed identical. If you can't, it isn't a 45-45-90 right triangle.
You can use a slightly-modified Pythagorean Theorem to determine the length of either of those legs:
Since it is conventional to not have a square root on the denominator of an answer:
Therefore, those two legs are each


