How do I find the value of sin 5pi / 6?
1 Answer
Aug 8, 2015
sin
Explanation:
Sin
Another way to think about it is to draw the angle in a Unit circle and create the "new" triangle in Quadrant II. 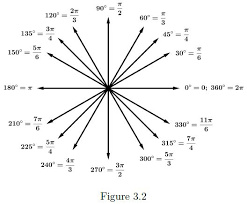
Drop a perpendicular to the x-axis and you will have the correct triangle to use.
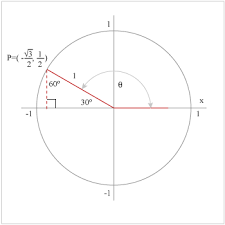
From this triangle, you need the opposite leg length, which is
Since the hypotenuse is equal to 1 in the Unit circle, the opposite leg length is the answer for sine. (dividing by 1 is not necessary)

