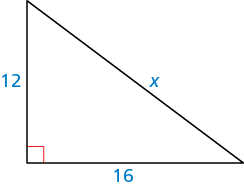
How do I find the value of x?Do the side lengths form a pythagorean triple?
3 Answers
Explanation:
Yes, the sides form a triple (it is a
By the Pythagorean Theorem,
In this case,
Explanation:
Use the Pythagorean theorem (
Lets label the right triangle such that:
Thus,
So our missing side,
We can now say that the sides of our triangle are
I've included a link that lists a couple of Pythagorean triples (a couple because they are infinitely many).



