Question

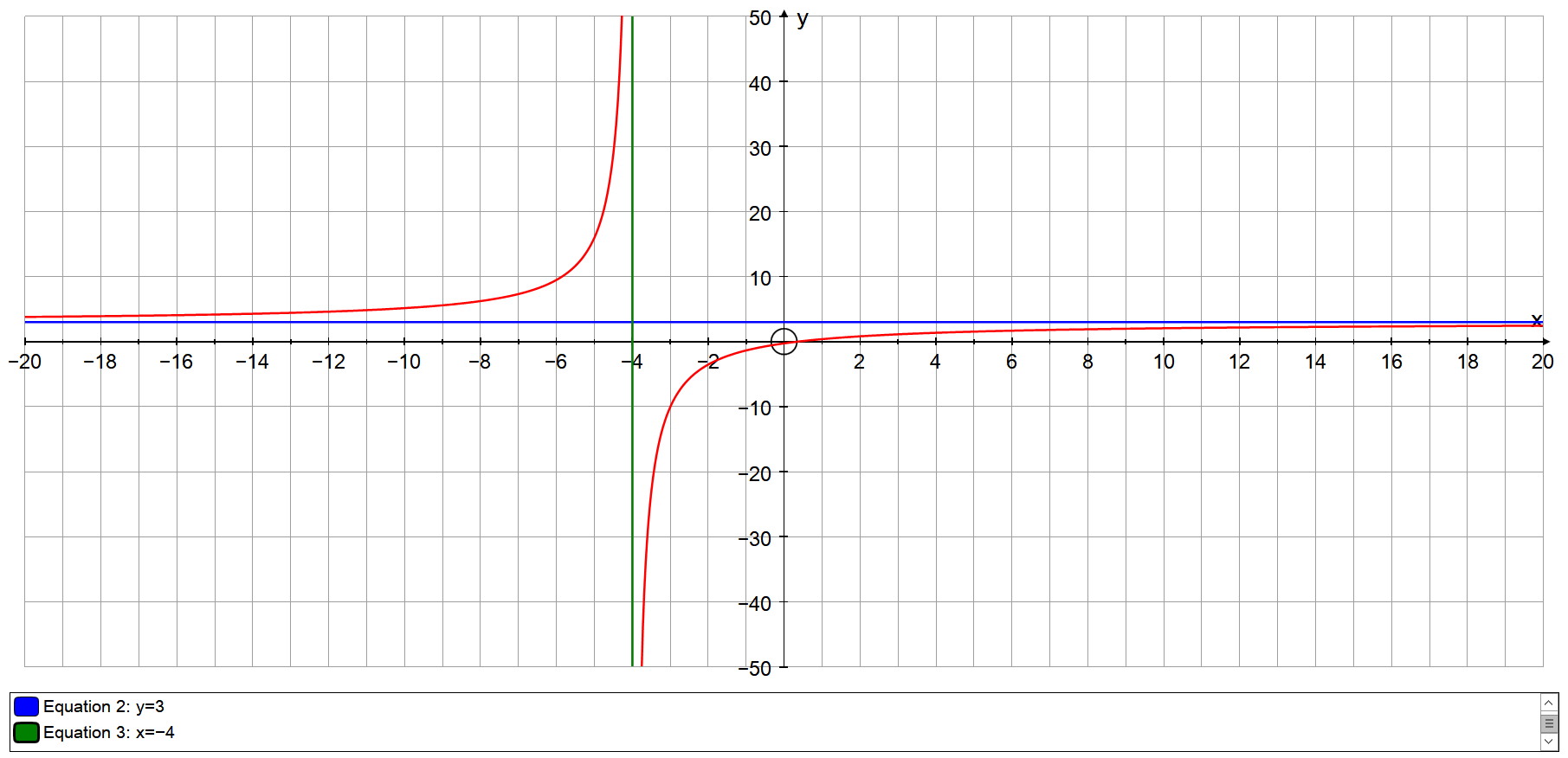
How do I find the vertical and horizontal asymptotes of the function `f(x)=(3x-1)/(x+4)`?

Answer 1

See below.

Explanation:

`f(x)=(3x-1)/(x+4)`

Vertical asymptotes occur where the function is undefined.

This happens when `x=-4`

So the line `color(blue)(x=-4)` is a vertical asymptote.

We next examine the end behaviour as `x->-+-oo`

Starting with:

`(3x-1)/(x+4)`

Divide by `x`:

`((3x)/x-1/x)/(x/x+4/x)`

Cancelling:

`((3cancel(x))/cancel(x)-1/x)/(cancel(x/x)+4/x)=(3-1/x)/(1+4/x)`

as `x->oo` , `(3-1/x)/(1+4/x)->(3-0)/(1+0)=3`

as `x->-oo` , `(3-1/x)/(1+4/x)->(3-0)/(1+0)=3`

This show that the line `color(blue)(y=3)` is a horizontal asymptote.

These findings are confirmed by the graph of `f(x)=(3x-1)/(x+4)`: