Polar coordinates are in the form #(r,theta)#. This basically means (radius,angle). To graph them, you have to find your #r# on your polar axis and then rotate that point in a circular path by #theta#. The convention is that a positive #r# will take you r units to the right of the origin (just like finding a positive #x# value), and that #theta# is measured counterclockwise from the polar axis.
#theta# is typically measured in radians, so you have to be familiar with radian angles to graph polar coordinates. However, it can be given in degrees. You can even convert between the two if you want to.
Alternatively, you could convert polar coordinates to rectangular coordinates #(x,y)# to graph the same point. To do this you can use the equations:
#x=rcos(theta)#
#y=rsin(theta)#
This is the relationship to show their equivalency:

Let's look at graphing #(r,theta)# without converting it. This is what the "axes" system looks like for polar coordinates with a polar coordinate graphed:
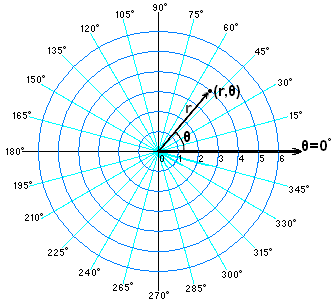
So, where #theta=0#, you have the "pole" or "polar axis." You begin at the origin (the middle of the circles), and mark down the point that is your #r# (or radius). Here, it looks like #r=4#. Note: You have to start with #r#, and then from there rotate by #theta#. Now that you have your #r#, you need to rotate that point in a circular path until you reach the angle given. Here, it seems that #theta# is a little over #pi/4#.

