Some calculators and software or websites will graph this for you:
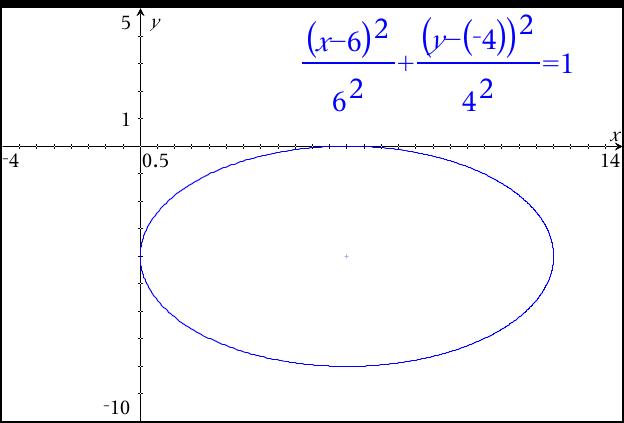
In order for you to graph this yourself on paper, you would need to know how to find the center and the horizontal and vertical radii for the ellipse.
#(x-h)^2/(a^2)+(y-k)^2/(b^2)=1# is the form that tells us this information. (h,k) is the center of your graph. In this case, (6, -4). You can even see in the image above that the form is written as #(y-(-4))^2# in order to maintain the subtraction form.
The #a^2# that is the x-denominator tells us how far right and left to move away from the center. In this example, 36 = #6^2#, so we move right and left 6 units from the center. This puts your endpoints at (12,-4) and (0,-4). You can call this your "diameter" since it is the longer total distance moved from center, otherwise known as the major axis.
The #b^2# under the y-term tells us how far up and down to move from the center. If you move up and down 4 units, your endpoints are (6,0) and (6, -8). This is your shorter distance, or the minor axis.
In conclusion, this ellipse is easy to graph because it is in a nice form to work with. Think of it as a distorted circle, so the radii for the horizontal direction and the vertical direction are different from each other.


