Question

How do I graph the equation `16x^2-9y^2+32x+18y-137=0` on a TI-83?

Answer 1

First you would have to complete the square on both variables, x and y:
`16x^2−9y^2+32x+18y−137=0`

Group together the x terms and y terms, and move the constant to the other side.
`16(x^2+2x) -9(y^2-2y)=137`

Now, complete the squares. Half of the linear coefficient, square it, add inside the parentheses on the left and multiply by the factored out number before adding to the right.

`16(x^2+2x+1) -9(y^2-2y+1)=137+16-9`

Completed squares are now factorable:

`16(x+1)^2-9(y-1)^2=144`

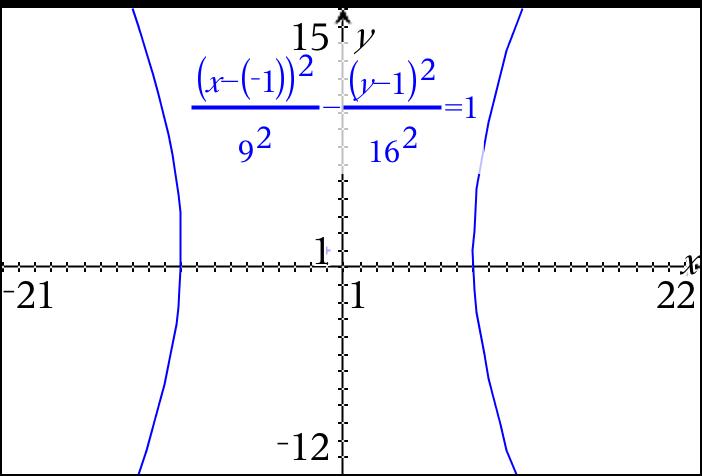
I can already tell by the form of the equation, that the graph will be a hyperbola. Now, when you solve for y = , there will be two parts to graph.
`-9(y-1)^2=144 - 16(x+1)^2`

Divide both sides by 9, and take the square root:

`sqrt((y-1)^2)=sqrt((144 - 16(x+1)^2)/9)`

So y - 1 = `+-sqrt((144 - 16(x+1)^2)/9)`

And last, add 1: y = `1+-sqrt((144 - 16(x+1)^2)/9)`

You will have to type in two separate equations into your calculator! (TI-83 or 84 models)
y1 = the part with the "+" sign
y2 = the part with the "-" sign

In other online applications or in the TI-nspire, you do not have to solve for y = any more. After this step: `16(x+1)^2-9(y-1)^2=144`
just divide both sides by 144 and simplify:
`((x+1)^2)/9-((y-1)^2)/16=1`
Here is what the TI-nspire looks like now: