How do I prove these couple of sets? thanks
a) #A ⊂ B <=> A ∪ B = B#
b) #(A - B) ∪ (B - A) = (A ∪ B) - (A ∩ B)#
a)
b)
1 Answer
See below.
Explanation:
a.)
Before a more formal proof, we can get an intuitive understanding about why this is true.
Here is a visualization:
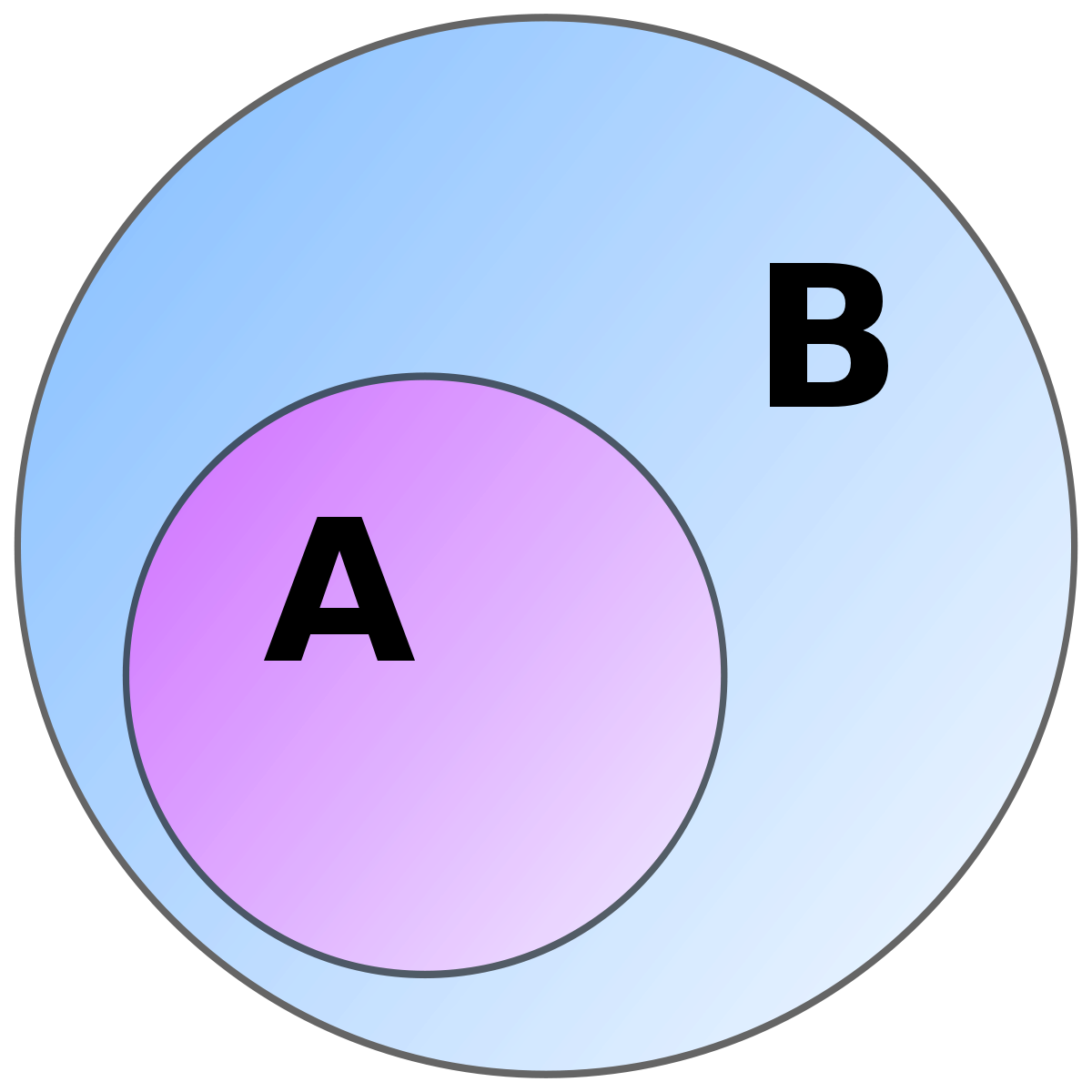
The next part (
The symbol between (
Let's look at how to prove this. Since it is an iff statement, we will have to prove it both ways.
Proof.
Let A and B be sets with
#A sub B# . Let#x in A# . Then, by definition of subset,#x in B# for all# x in A# . So, if#x in B# , then#x in A uu B# .Now let
#x in A uu B# . Then#x in A# or#x in B# . If#x in B# , then clearly this statement is true. If#x in A# , then it must be that#x in B# , since#A sub B# . In either case,#x in B# .We have shown that if
#A sub B# then#A uu B sub B# and#B sub A uu B# . Hence,#A uu B = B# .Now assume
#A uu B = B# . Let#x in A# be an arbitrary element. Since#x in A# , it follows that#x in A# or#x in B# . Equivalently,#x in A uu B# . But#A uu B= B# . Hence,#x in B# .#square#
b.)
Proof.
Let A and B be sets and let
#x in ((A-B)uu(B-A))# . Then, by definition of union,#x in (A-B)# or#x in (B-A)# .If
#x in (A-B)# , then#x in A# and#x !in B# , by definition of complement. If#x in (B-A)# , then#x in B# and#x !in A# . Then it follows that#x in B# or#x in A# , or it must be that#x in A^c# or#x in B^c# . Equivalently,#x !in (AuuB)# or,#x in (A nn B)^c# . Hence,#x in ((AuuB)-(AnnB))# by definition of complement.Now let
#x in ((AuuB)-(AnnB))# . Then#x in (A uu B)# and#x in bar(AnnB)# , by definition of complement. Therefore#x in A# or#x in B# , and#x in (A-B)# or#x in (B-A)# . Equivalently (removing the redundancy),#x in ((A-B)uu(B-A))# .
#:. (A-B)uu(B-A) = (AuuB)-(AnnB) square#
Drawing venn diagrams is a great way to visualize these types of statements and to make sense of them as you go. If you're unsure of any of the above claims, try drawing a picture.

