[1] Ideal Gas EoS: #\quad PV=nRT;# (always true)
[2] Monoatomic ideal gases: If #U# is the internal energy, #C_p# and #C_v# are molar heat capacities at constant volume and constant pressure, respectively,
#U=3/2 nRT#
#C_p = 5/2R;\qquad C_v=3/2R;\qquad \gamma=C_p/C_v=5/3;#
[3] Adiabatic Process:
EoS: #\quad PV^\gamma = const.# (true only for adiabatic process)
Work Done: #W_{i\rightarrowf}=(p_fV_f-p_iV_i)/(\gamma-1)#
Problem
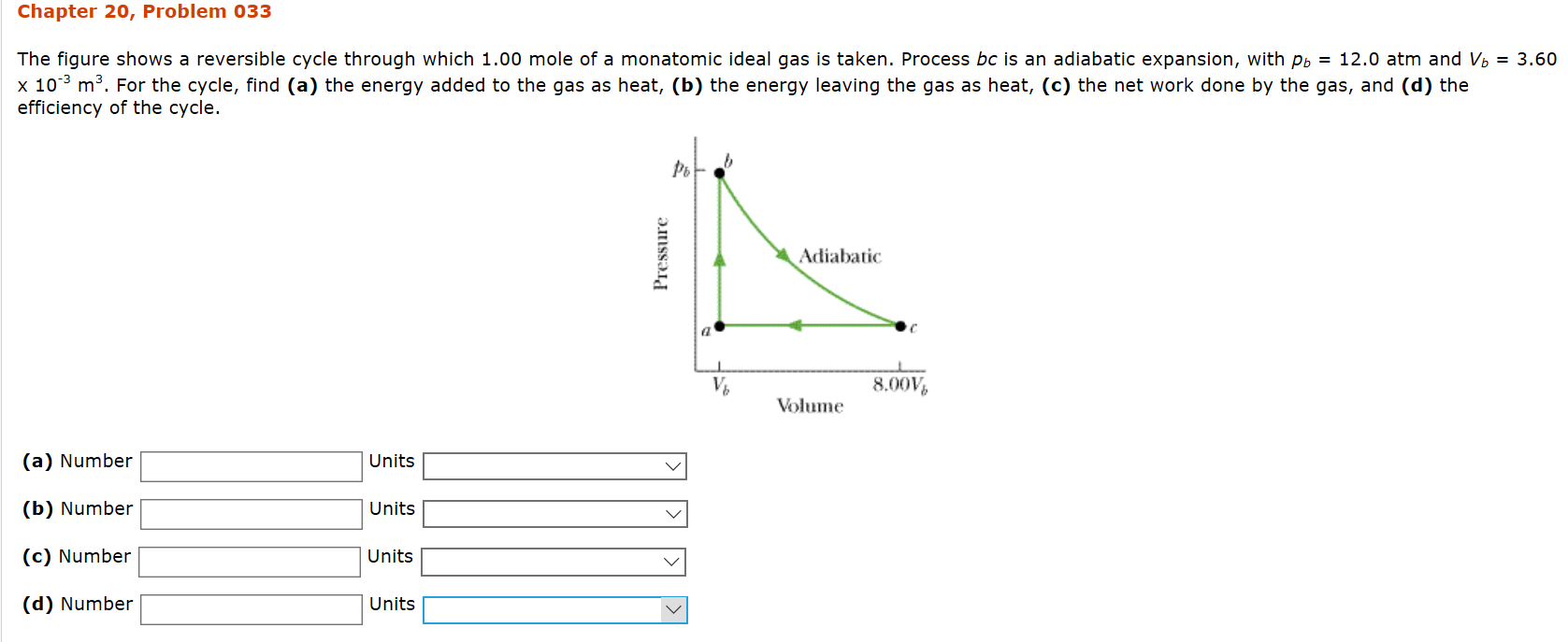
The three intermediate points #a#, #b# and #c# are characterized by the state variables #(p_a, V_a); \quad(p_b, V_b)# and #(p_c, V_c)#.
Observe that: #\quad V_a=V_b# and #\quadp_a=p_c#
Step 1 (Adiabatic Expansion): During adiabatic process the system does not exchange heat with the surroundings.
#Q_{bc}=0;#
#p_bV_b^\gamma = p_cV_c^\gamma; \qquad \rightarrow p_c/p_b = (V_b/V_c)^\gamma#
Remember that #\quad p_a=p_c# and #V_c=8V_b=8V_a#,
#p_c/p_b=1/8^\gamma=p_a/p_b#......(Eq1)
Next calculate the work done -
#W_{bc} = (p_cV_c-p_bV_b)/(\gamma-1)=(p_bV_b)/(\gamma-1)[(p_cV_c)/(p_bV_b)-1]#
#W_{bc}=-(p_bV_b)/(\gamma-1)[1-1/8^(\gamma-1)]#......(Eq2)
Work done is negative, as is expected for expansion. Work is being done by the gas.
Step 2 (Isobaric Compression): For isobaric processes the ratio of volume to temperature is a constant (Charles's law).
#V_c/T_c = V_a/T_a; \qquad \rightarrow T_c/T_a = V_c/V_a=8#
Change in internal energy -
#\Delta U_{ca}=3/2nR\DeltaT_{ca}=3/2nR(T_a-T_c)=3/2nRT_a(1-T_c/T_a)#
#\Delta U_{ca}=3/2nRT_a(1-8)=-21/2(nRT_a)#
Using the ideal gas equation of state, #\quad p_aV_a=nRT_a# and recognizing that #V_a=V_b#,
#\DeltaU_{ca}=-21/2p_aV_a=-21/2p_aV_b#
Using Eq1 : #\quadp_a=p_b/8^\gamma#
#\DeltaU_{ca} = -21/2(p_b/8^\gamma)V_b=-21/2(p_bV_b)/8^\gamma#......(Eq3)
Work done during an isobaric process is-
#W_{ca}=-p_a\DeltaV_{ca}=-p_a(V_a-V_c)=p_a(V_c-V_a)#
#W_{ca}=p_aV_a(V_c/V_a-1)=p_aV_a(8-1)=7p_aV_a#
Using Eq1: #\quad p_a=p_b/8^\gamma# and the fact that #V_a=V_b#,
#W_{ca} = 7(p_b/8^\gamma)V_b=7(p_bV_b)/8^\gamma#......(Eq4)
Work done is positive, as it is expected for compression. Work is being done on the gas.
Next apply the first law of thermodynamics to calculate the heat,
#\Delta U_{ca}=Q_{ca}+W_{ca}; \qquad Q_{ca}=\DeltaU_{ca}-W_{ca}#
#Q_{ca} = -(21/2 +7)(p_bV_b)/8^\gamma=-35/(2\times8^\gamma)p_bV_b# ......(Eq 5)
Negative value for #Q_{ca}# indicates that heat leaves the system.
Step 3 (Isochoric Heating): For an isochoric process volume is a constant and the ratio of pressure to temperature is a constant. Since the volume of the gas does not change, the work done during an isochoric process is zero.
#W_{ab}=0;#
#p_a/T_a = p_b/T_b; \qquad \rightarrow T_a/T_b = p_a/p_b=1/8^\gamma;#
The temperature the gases raises from #T_a# to #T_b#. So heat must have entered the system. Use the temperature difference and molar heat capacity for constant volume process to find this heat
#Q_{ab} = nC_v\Delta_{ab}=nC_v(T_b-T_a)=nC_vT_b(1-T_a/T_b)#
#Q_{ab}=n(3/2R)T_b(1-1/8^\gamma)=3/2(nRT_b)(1-1/8^\gamma)#
Using the ideal gas EoS : #\quadp_bV_b=nRT_b#,
#Q_{ab} = 3/2(1-1/8^\gamma)p_bV_b# ...... (Eq 6)
As expected, #Q_{ab}# is positive, indicating that heat is added to the system.
Numerical Calculation:
#p_b = 12\quadatm = (12 \quadcancel(atm))\times(1.01325\times10^5\quad (Pa)/(cancel{atm}))#
#p_b = 1.21\times10^6\quad N/m^2; \qquad V_b = 3.60\times10^{-3}\quadm^3;#
#p_bV_b = 4.35\times10^3\quadN.m = 4.35 \quadkJ#.
#\gamma = 5/3#
(a) Heat added to the gas:
#Q_{ab}=3/2(1-1/8^\gamma)p_bV_b = +6.32\quad kJ;#
(b) Heat leaving the gas:
#Q_{ca}=-35/(2\times8^\gamma)p_bV_b = -2.38\quad kJ;#
(c) Net Work Done:
#W_{bc}=-(p_bV_b)/(\gamma-1)[1-1/8^{\gamma-1}]=-4.89\quad kJ;#
#W_{ca}=+0.95\quad kJ;#
#W_{"net"}=W_{bc}+W_{ca}=-3.94\quad kJ#
Negative sign is because the work is done by the gas. Negative sign is as a result of sign convention, according to which the work done on the gas is positive and the work done by the gas is negative.
(d) Efficiency of the cycle:
#\eta\equiv |W|/Q_{"in"}=(|Q_{"in"}|-|Q_{"out"}|)/Q_{"in"}=1-|Q_{"out"}|/Q_{"in"}=1-|Q_{ca}|/Q_{ab}#
#\eta=62.3%#