How do I use Pascal's triangle to expand (x + 2)^5?
1 Answer
Jul 9, 2015
You write out the sixth row of Pascal's triangle and make the appropriate substitutions.
Explanation:
Pascal's triangle is
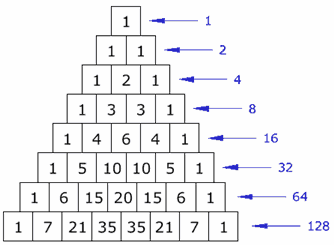
The numbers in the fifth row are 1, 5, 10, 10, 5, 1.
They are the coefficients of the terms in a fifth order polynomial.
But our polynomial is

