Pascal's Triangle and Binomial Expansion
Key Questions
-
The expansion of a binomial is given by the Binomial Theorem:
#(x+y)^n=( (n), (0) )*x^n+( (n), (1) )*x^(n-1)*y^1+...+( (n), (k) )*x^(n-k)*y^k+...+( (n), (n) )*y^n = sum_(k=0)^n*( (n), (k) )*x^(n-k)*y^k #
where#x, y in RR# ,#k, n in NN# , and#( (n), (k) )# denotes combinations of#n# things taken#k# at a time.# ( (n), (k) )*x^(n-k)*y^k # is the general term of the binomial expansion.We also have the formula:
#( (n), (k) )=(n!)/(k!*(n-k)!)# , where#k! = 1*2*...*k# We have three cases:
Case 1: If the terms of the binomial are a variable and a constant
#(y=c# , where#c# is a constant), we have#(x+c)^n=( (n), (0) )*x^n+( (n), (1) )*x^(n-1)*c^1+...+( (n), (k) )*x^(n-k)*c^k+...+( (n), (n) )*c^n # We can see that the constant term is the last one:
#( (n), (n) )*c^n#
(as#( (n), (n) )# and#c^n# are constant, their product is also a constant).Case 2: If the terms of the binomial are a variable and a ratio of that variable (
#y=c/x# , where#c# is a constant), we have:
# (x+c/x)^n=( (n), (0) )*x^n + ( (n), (1) )*x^(n-1)*(c/x)^1+...+( (n), (k) )*x^(n-k)*(c/x)^k+...+( (n), (n) )*(c/x)^n # This time, we see that the constant term is not to be found at the extremities of the binomial expansion. So, we should have a look at the general term and try to find out when it becomes a constant:
# ( (n), (k) )*x^(n-k)*(c/x)^k=( (n), (k) )*x^(n-k)*c^k*1/x^k = (( (n), (n) )*c^k)*(x^(n-k))/x^k = (( (n), (k) )*c^k)*x^(n-2k) # .We can see that the general term becomes constant when the exponent of variable
#x# is#0# . Therefore, the condition for the constant term is:#n-2k=0 rArr# #k=n/2# . In other words, in this case, the constant term is the middle one (#k=n/2# ).Case 3: If the terms of the binomial are two distinct variables
#x# and#y# , such that#y# cannot be expressed as a ratio of#x# , then there is no constant term . This is the general case#(x+y)^n# 
-
Answer:
See explanation...
Explanation:
The Binomial Theorem for positive integer powers can be written:
#(a+b)^n = sum_(k=0)^n ((n),(k)) a^(n-k) b^k# where
#((n),(k)) = (n!)/(k! (n-k)!)# Note that some people like to call the first row of Pascal's triangle the
#0# th. Others like me prefer to call it the#1# st.Counting from
#1# , the#n+1# st row of Pascal's triangle consists of the numbers#((n),(0)), ((n),(1)), ... ((n), (n))# .So rather than 'calculate' the individual coefficients for
#(a+b)^n# , you can read them off from the#(n+1)# st row of Pascal's triangle...
For example, if we were calculating
#(a+b)^12# then the coefficients would be#1# ,#12# ,#66# ,#220# ,...,#1# .Typically our
#a# and#b# are not plain variables, but have a multiplier, e.g.#(2a+3b)^n# . In such a case you need to multiply the binomial coefficient by a suitable multiple of the powers of#(2a)# and#(3b)# , e.g.#((n),(k)) (2a)^(n-k) (3b)^k = ((n),(k))2^(n-k)3^k a^(n-k) b^k# , etc. -

One of the most interesting Number Patterns is Pascal's Triangle. It is named after Blaise Pascal.
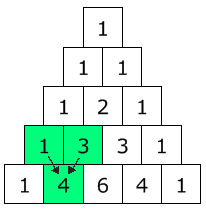
To build the triangle, always start with "1" at the top, then continue placing numbers below it in a triangular pattern.
Each number is the two numbers above it added together (except for the edges, which are all "1").
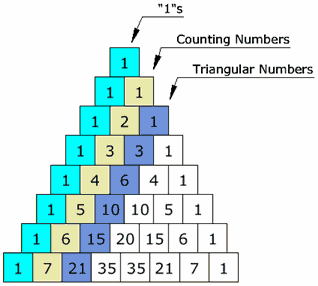
Interesting part is this:
The first diagonal is just "1"s, and the next diagonal has the counting numbers. The third diagonal has the triangular numbers. The fourth diagonal has the tetrahedral numbers.
Many interesting things about this topic you can look here.
-
Answer:
Rows of Pascal's triangle provide the coefficients to expand
#(a+b)^n# as follows...Explanation:
To expand
#(a+b)^n# look at the row of Pascal's triangle that begins#1, n# . This provides the coefficients.
For example,
#(a+b)^4 = a^4+4a^3b+6a^2b^2+4ab^3+b^4# from the row#1, 4, 6, 4, 1# How about
#(2x-5)^4# ?Let
#a = 2x# and#b = -5# .Then:
#(2x-5)^4 = (a+b)^4 = a^4+4a^3b+6a^2b^2+4ab^3+b^4# #=(2x)^4+4(2x)^3(-5)+6(2x)^2(-5)^2+4(2x)(-5)^3+(-5)^4# #=16x^4+4(8x^3)(-5)+6(4x^2)(25)+4(2x)(-125)+(625)# #=16x^4-160x^3+600x^2-1000x+625#