Question

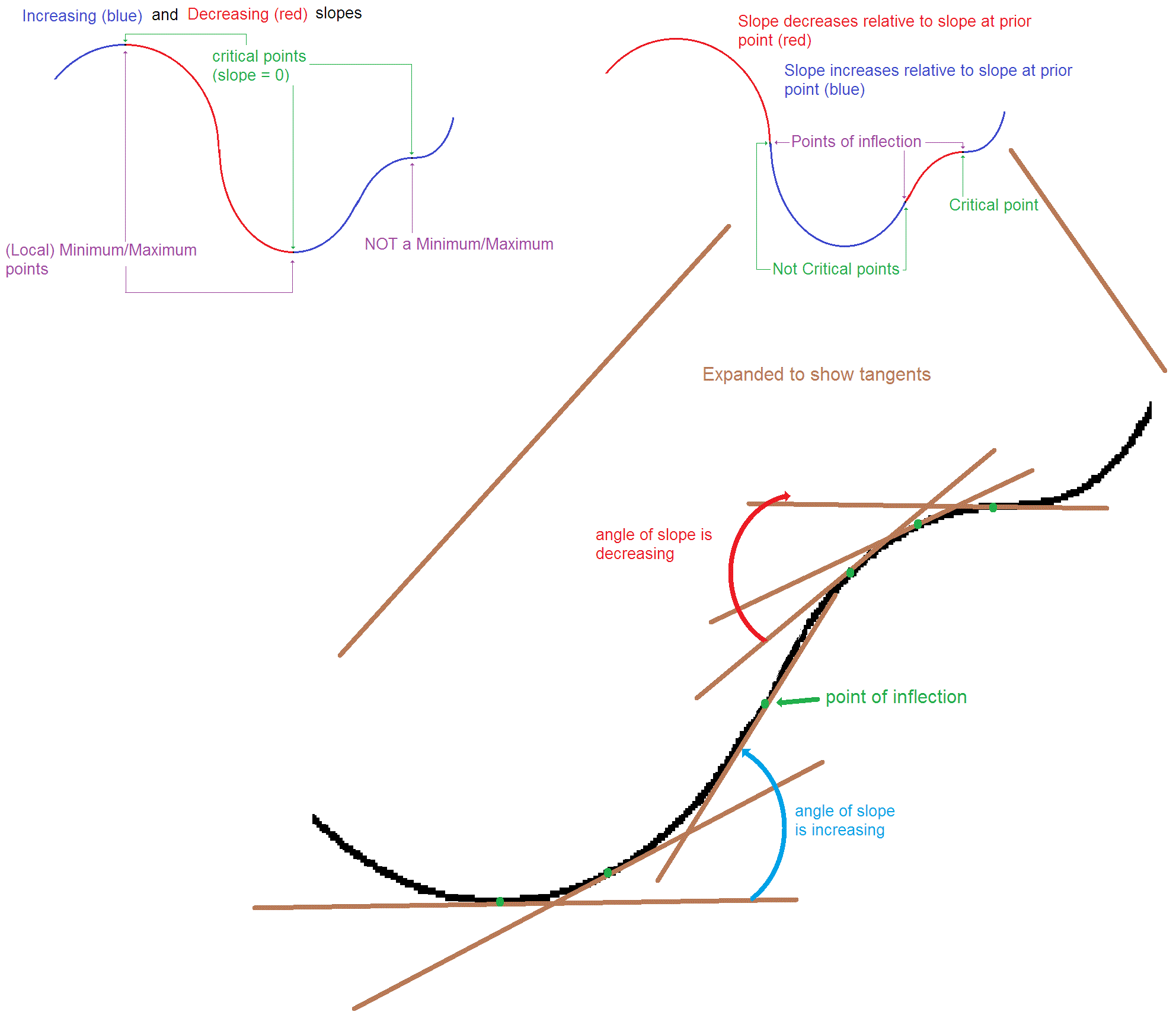
How do inflection points differ from critical points?

Answer 1

Inflection points occur when the rate of change in the slope changes from positive to negative or from negative to positive. Inflection is related to rate of change of the rate of change (or the slope of the slope).

Critical points occur when the slope is equal to `0`; that is whenever the first derivative of the function is zero. A critical point may or may not be a (local) minimum or maximum.

It is not necessary for the slope to be `0` for a point of inflection to occur (it may or may not).

The second derivative must be `0` for a point of inflection, but that is not by itself sufficient; the rate of change of the slope must change between positive and negative.