How do solve applications of differentiation?
A builder needs to get a long ladder around the corner of a corridor.
There are some restrictions:
the corridors are 4m and 5m wide and meet at right angles
the ladder has to stay horizontal (parallel to floor or ceiling)
the ladder can't bend, it is rigid.
Find the longest length of the ladder that can be manoeuvred around the corner of the corridor.
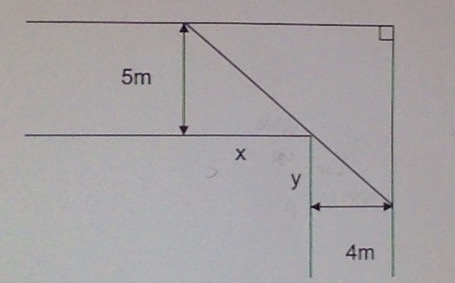
Hint: use similar triangles and express length of ladder in terms of x.
A builder needs to get a long ladder around the corner of a corridor.
There are some restrictions:
the corridors are 4m and 5m wide and meet at right angles
the ladder has to stay horizontal (parallel to floor or ceiling)
the ladder can't bend, it is rigid.
Find the longest length of the ladder that can be manoeuvred around the corner of the corridor.

Hint: use similar triangles and express length of ladder in terms of x.
1 Answer
Explanation:
The answer given assumes of course that the ladders thickness can be ignored or assumed to be infinitesimal.
From the dimensions of the similar triangles , given in the sketch supplied,
The ladders length will be the sum of the lengths of two hypotenuse formed by the two similar triangles, i.e
Substituting
So from.......
Checking the second derivative is negative will confirm that this value of
Hope this helps.

