Question

How do you apply trigonometric equations to solve real life problems?

Answer 1

When at `(71.06047^circ W, 43.08350^circ N)` a distant cell tower is at heading `131^circ (SE)`, and at `(71.06137^circ W, 43.08007^circ N)` it's at heading `99^circ (E)`. Where is the tower?

Explanation:

Someone from San Antonio requested an answer three years ago! Hope they've figured it out by now.

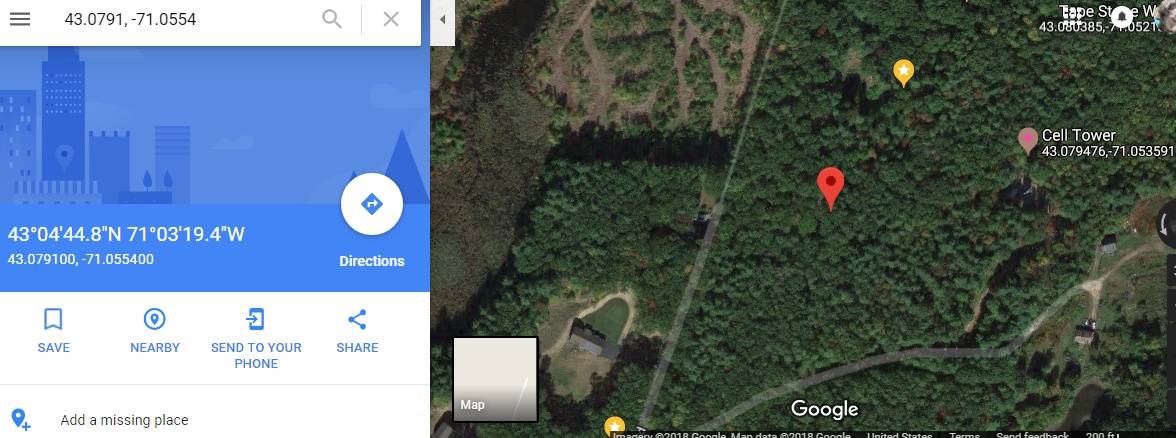
Here some real life trig I've been meaning to do. I wanted to know where that cell phone tower I can see from my house is. It's on a hill in the distance.

From one spot near my house, maybe the one in this picture, I pointed my phone at the tower with my GPS app on and got this:

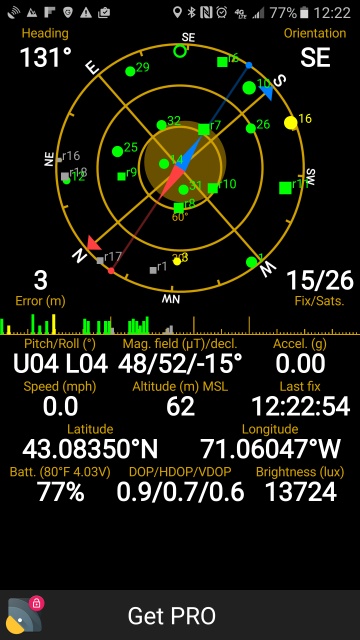
The relevant information is:

`(71.06047^circ W, 43.08350^circ N)` heading `131^circ (SE)`

At another spot I got

`(71.06137^circ W, 43.08007^circ N)` heading `99^circ (E)`

The heading is relative to due north. Here's a figure.

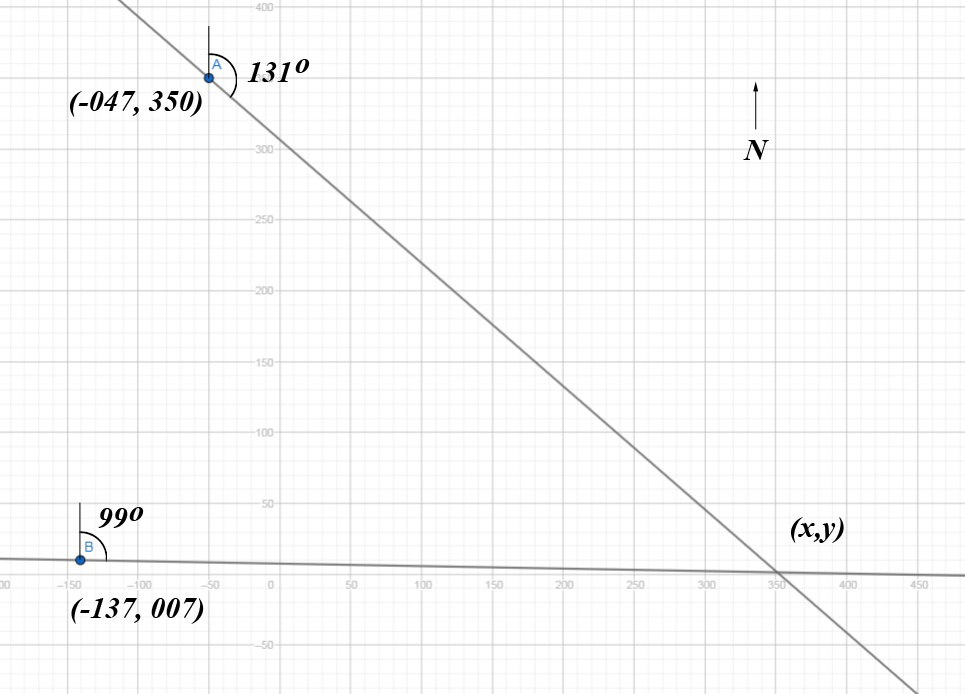
We treat west as negative. I translated the origin to #(-71.06, 43,08) and multiplied the coordinates by 100,000 so our new problem is:

`(-047, 350)` heading `131^circ (SE)`

`(-137, 007)` heading `99^circ (E)`

Find Tower coordinates `(x,y)`

To solve we write the equations of the two lines and find the meet.

When measured relative to the y axis like that, the heading angle `theta` converts to a slope as `m = cot theta`.

So our two lines

`y - 350 = (x+47) cot 131`

`(y - 7)= (x+137) cot 99`

meet when

# 350 + (x+47) cot 131 = 7+ (x+137) cot 99 #

`x= {7 + 137 cot 99 -350 - 47 cot 131} /{cot 131 - cot 99}` x

`x≈ 455.537`

`y ≈-86.849`

That means my tower is at GPS coordinates

`(-71.06 +.00456, 43.08 - .000868) = (-71.0554, 43.07132)`

Let's check Google Maps. Pretty good, off by around 400 feet.