Products, Sums, Linear Combinations, and Applications
Key Questions
-
Main approach to solve a trig equation : Use Trig Transformation Identities to transform it to a product of a few basic trig equations. Solving a trig equation finally results in solving a few basic trig equations.
Transformation Trig Identities that convert Sums to Products .
1. cos a + cos b = 2cos (a +b)/2cos (a - b)/2
2. cos a - cos b = -2sin (a + b)/2sin (a - b)/2
3. sin a + sin b = 2sin (a + b)/2cos (a - b)/2
4. sin a - sin b = 2cos (a + b)/2sin (a - b)/2
5. tan a + tan b = sin (a + b)/cos acos b.
6. tan a - tan b = sin (a - b)/cos acos b
Example 1 . Transform f(x) = sin a + cos a to a product.
Solution. Use Identity (3) to transform f(x) = sin a + sin (Pi/2 - a) = 2sin (Pi/4)sin (a + Pi/4)
Example 2 . Transform f(x) = sin x + sin 3x + sin 2x to a product. Use Identity (3) to transform the sum (sin x + sin 3x), then put in common factor.
f(x) = (2sin 2acos a) + 2sin acos a = 2cos a(2sin 3a/2*cos a/2) -
Answer:
Substitute
a cos x + b sin x = sqrt{a^2 + b^2} cos(x -text{arctan2}( b //, a) ) where arctan2 is the two parameter, four quadrant inverse tangent.
Explanation:
I've been answering all these old math questions. It's hard to know if anyone reads the answers.
The linear combination of a cosine and a sine of the same angle corresponds to a scaling and a phase shift. Let's explain how that works.
The linear combination of a cosine and a sine of the same angle is an expression of the form:
a cos x + b sin x That looks very much like the sum angle formula for sine or the difference angle formula for cosine:
sin(alpha + beta ) = sin alpha cos beta + cos alpha sin beta cos(alpha - beta) = cos alpha cos beta + sin alpha sin beta Indeed, we can take our linear combination and transform it into a scaled version of either of these. Pro Tip: When given a choice, prefer cosine to sine.
Let's multiply by a scale factor
r and setalpha = x, beta=theta. r cos(x - theta) = r cos theta cos x + r sin theta sin x Matching to our linear combination leads us to want to solve for
r andtheta :a = r cos theta b = r sin theta We've seen this before. It's how we turn turn the polar coordinates
P(r, theta) to rectangular coordinates, here(a,b). So our task is to turn(a,b) to polar coordinates.Let's remind ourselves how to do that, perhaps in a bit more detail than usually seen.
Squaring and adding we get
a^2 + b^2 = (r cos theta)^2 + (r sin theta)^2 = r^2(cos^2 theta + sin^2 theta) = r^2 r = sqrt{a^2 + b^2} sin theta = b/r cos theta = a/r tan theta = b/a theta = text{arctan2}( b //, a) Usually this is written as the regular arctangent, but that's not really right. The regular arctangent only covers two quadrants, and doesn't work on the y axis. This is the two parameter, four quadrant inverse tangent, which returns a valid theta for all real input pairs. The
//, is deliberate, reminding us there are two separate parameters, and which is which.So now we're assured
a = r cos theta andb = r sin theta soa cos x + b sin x = r cos theta cos x + r sin theta sin x = r cos(x - theta) a cos x + b sin x = sqrt{a^2 + b^2} cos(x -text{arctan2}( b //, a) ) -
Answer:
When at
(71.06047^circ W, 43.08350^circ N) a distant cell tower is at heading131^circ (SE) , and at(71.06137^circ W, 43.08007^circ N) it's at heading99^circ (E) . Where is the tower?Explanation:
Someone from San Antonio requested an answer three years ago! Hope they've figured it out by now.
Here some real life trig I've been meaning to do. I wanted to know where that cell phone tower I can see from my house is. It's on a hill in the distance.

From one spot near my house, maybe the one in this picture, I pointed my phone at the tower with my GPS app on and got this:
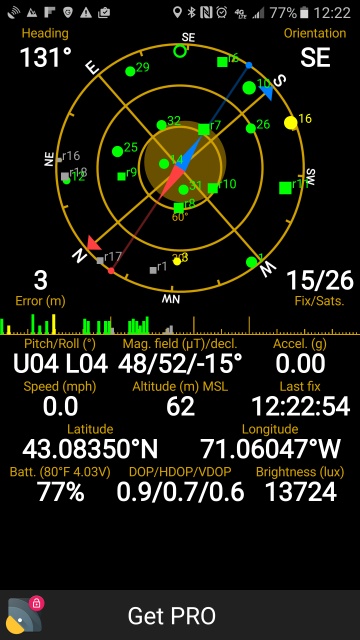
The relevant information is:
(71.06047^circ W, 43.08350^circ N) heading131^circ (SE) At another spot I got
(71.06137^circ W, 43.08007^circ N) heading99^circ (E) The heading is relative to due north. Here's a figure.
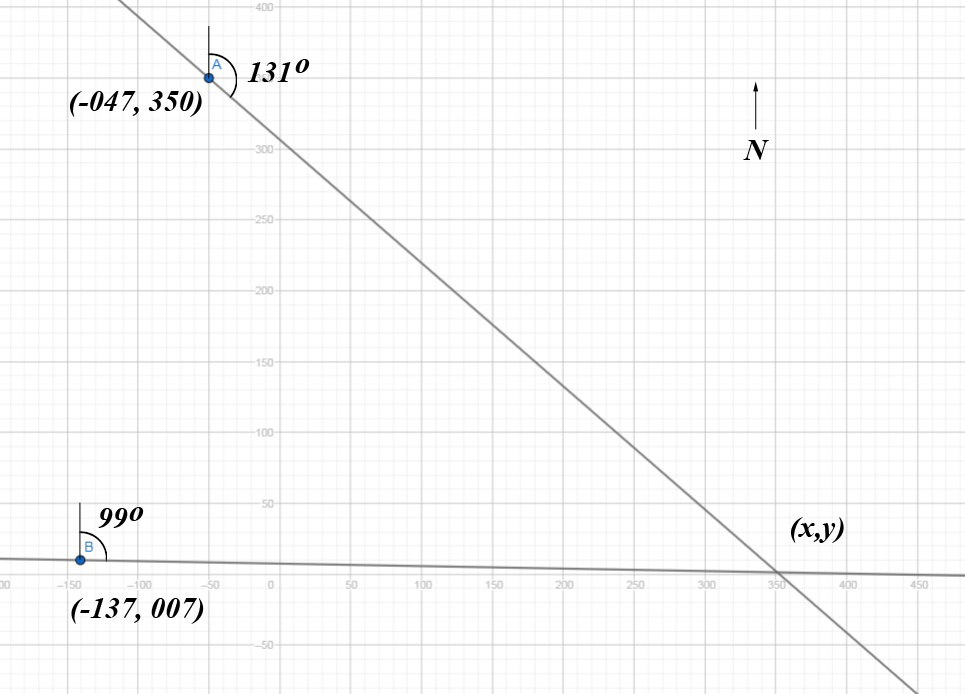
We treat west as negative. I translated the origin to #(-71.06, 43,08) and multiplied the coordinates by 100,000 so our new problem is:
(-047, 350) heading131^circ (SE) (-137, 007) heading99^circ (E) Find Tower coordinates
(x,y) To solve we write the equations of the two lines and find the meet.
When measured relative to the y axis like that, the heading angle
theta converts to a slope asm = cot theta .So our two lines
y - 350 = (x+47) cot 131 (y - 7)= (x+137) cot 99 meet when
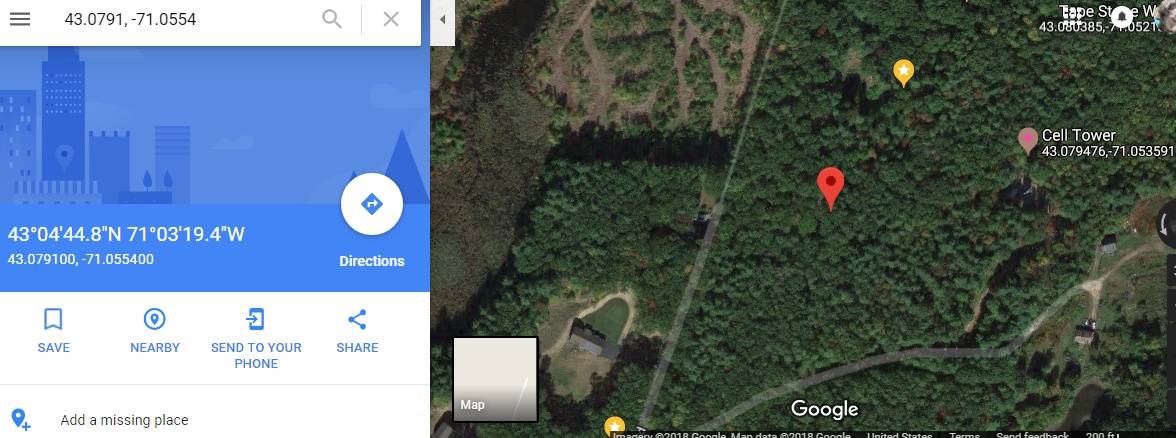
350 + (x+47) cot 131 = 7+ (x+137) cot 99 x= {7 + 137 cot 99 -350 - 47 cot 131} /{cot 131 - cot 99} xx≈ 455.537 y ≈-86.849 That means my tower is at GPS coordinates
(-71.06 +.00456, 43.08 - .000868) = (-71.0554, 43.07132) Let's check Google Maps. Pretty good, off by around 400 feet.
-
Answer:
As below.
Explanation:
color(blue)("Sum to Product Formulas"
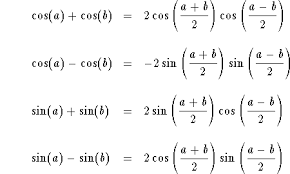
(
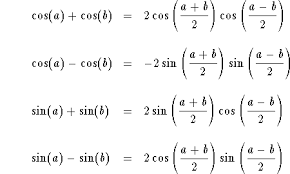 )
) color(green)("Product to Sum Formulas"
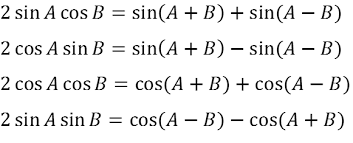
(
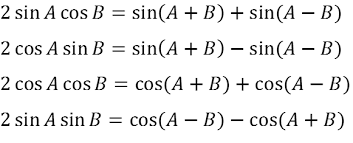 )
)