How do you calculate deadweight loss?
1 Answer
It depends on the subject you're dealing with: taxes or subsidies. Either way, deadweight loss measures the loss of efficiency in a market. That happens because of the government revenue (or expenditure, in the case of subsidy) as well as the difference between the price paid by consumers and the price actually received by the producers. This difference can be stated as
#P^d# is the price paid by demand (consumers)#P^s# is the price paid by supply (producers)#t# stands for the excise tax value (or proportion, when it's ad valorem)
Graphically, the situation is understood as follows:
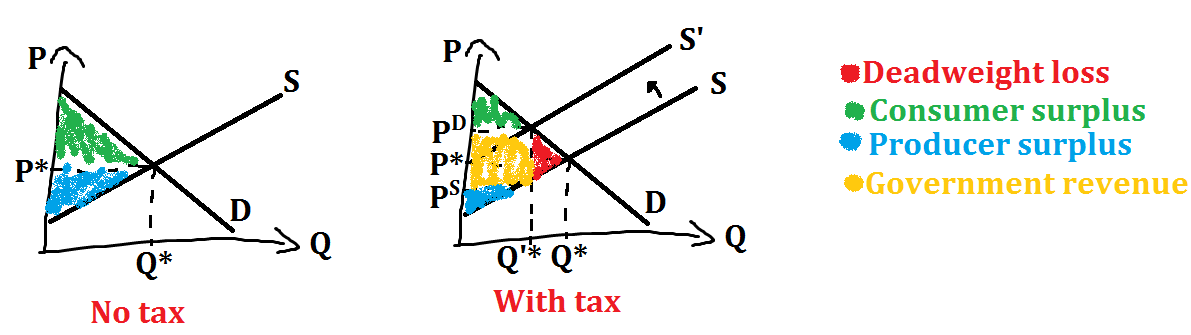
The calculation behind it will really depend on the exercise/situation you're dealing with. In general terms, however, we can draw a way to solve this.
The demand is generically given by
The supply is generically given by
Before taxes/subsidies, both
Drawing from our fundamental relation,
You just need to substitute one of these in the respective function (demand or supply), find its value (consider that
P.s.: For any more details in this topic, do not hesitate before asking more stuff. It's really prolific matter, so I'll end up this answer here, but do not consider the topic covered!
