How do you calculate Tan (sin^-1 (2/3)) ?
2 Answers
Aug 29, 2015
Explanation:
Drawing the right angled triangle, you realise that length of opposite side
Thus
Aug 29, 2015
Explanation:
If
then
And we have one of the defining triangles below: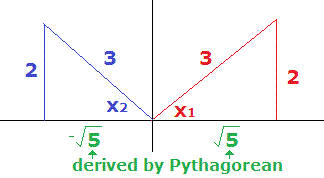
from which it follows:

