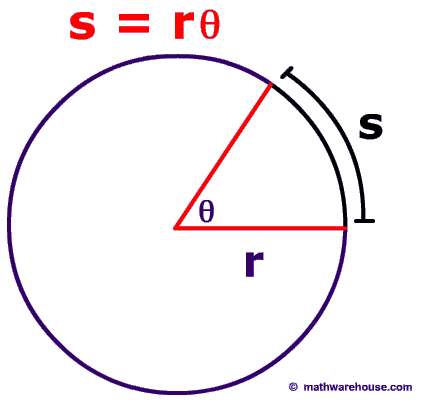For any #theta#, the length of the arc is given by the formula (if you work in radians, which you should:
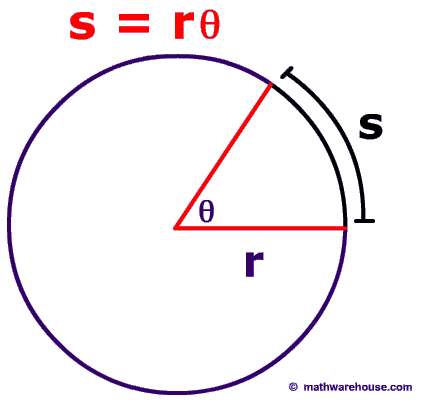
The area of the sector is given by the formula #(theta r^2)/2#
Why is this?
If you remember, the formula for the perimeter of a circle is #2pir#.
In radians, a full circle is #2pi#. So if the angle #theta = 2pi#, than the length of the arc (perimeter) = #2pir#. If we now replace #2pi# by #theta#, we get the formula #S = rtheta#
If you remember, the formula for the area of a circle is #pir^2#.
If the angle #theta = 2pi#, than the length of the sector is equal to the area of a circle = #pir^2#. We've said that #theta = 2pi#, so that means that #pi = theta/2#.
If we now replace #pi# by #theta/2#, we get the formula for the area of a sector: #theta/2r^2#