Applications of Radian Measure
Key Questions
-
In physics you use radians to describe circular motion, in particular you use them to determine angular velocity,
#omega# .
You may be familiar with the concept of linear velocity given by the ratio of displacement over time, as:
#v=(x_f-x_i)/t#
where#x_f# is the final position and#x_i# is the initial position (along a line).
Now, if you have a circular motion you use the final and initial ANGLES described during the motion to calculate velocity, as:
#omega=(theta_f-theta_i)/t#
Where#theta# is the angle in radians.
#omega# is angular velocity measured in rad/sec.
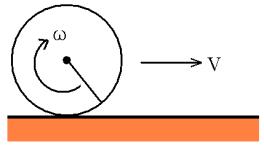
(Picture source: http://francesa.phy.cmich.edu/people/andy/physics110/book/chapters/chapter6.htm)Have a look to other rotational quantities you'll find a lot of ...radians!
-
For any
#theta# , the length of the arc is given by the formula (if you work in radians, which you should:
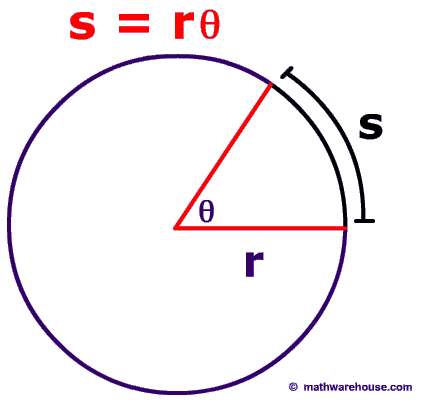
The area of the sector is given by the formula#(theta r^2)/2# Why is this?
If you remember, the formula for the perimeter of a circle is#2pir# .
In radians, a full circle is#2pi# . So if the angle#theta = 2pi# , than the length of the arc (perimeter) =#2pir# . If we now replace#2pi# by#theta# , we get the formula#S = rtheta# If you remember, the formula for the area of a circle is
#pir^2# .
If the angle#theta = 2pi# , than the length of the sector is equal to the area of a circle =#pir^2# . We've said that#theta = 2pi# , so that means that#pi = theta/2# .
If we now replace#pi# by#theta/2# , we get the formula for the area of a sector:#theta/2r^2# -
Let's call the cord
#AB# and the centre of the circle#C# Then if you divide the cord in half at
#M# you get two equal, but mirrored triangles#Delta CMA# and#Delta CMB# . These are both rectangular at#M# . (You should draw this yourself right now !).#angle ACM# is half the central angle that was given
(and#angleBCM# is the other half)Then
#sin angle ACM=(AM)/(AC) ->AM=AC*sin angle ACM# Since you know the radius
#(AC)# and the central angle (remember#angleACM=# half of that), you just plug in these values to get an accurate result for half the chord (so don't forget to double it for your final answer) -
Answer:
See examples in explanation
Explanation:
Earth's day/night spin about it axis is with
angular speed =
#2pi# radian / 24-hour day.Earths revolution about Sun is owith
angular speed = #2pi) radian / 365.26-day year.
Rotors making electro-mechanical rotations have high angular
speeds of
#kKpi# radian / minute, k > 1,making thousands of rpm ( revolutions / minute ).
,