How do you convert #2=(-x-3y)^2-5y+7x# into polar form?

Question

1400 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-02T19:53:58

Substitute #rcos(theta)# for x and #rsin(theta)# for y and then simplify to a quadratic in r.
Use the positive root of the quadratic formula

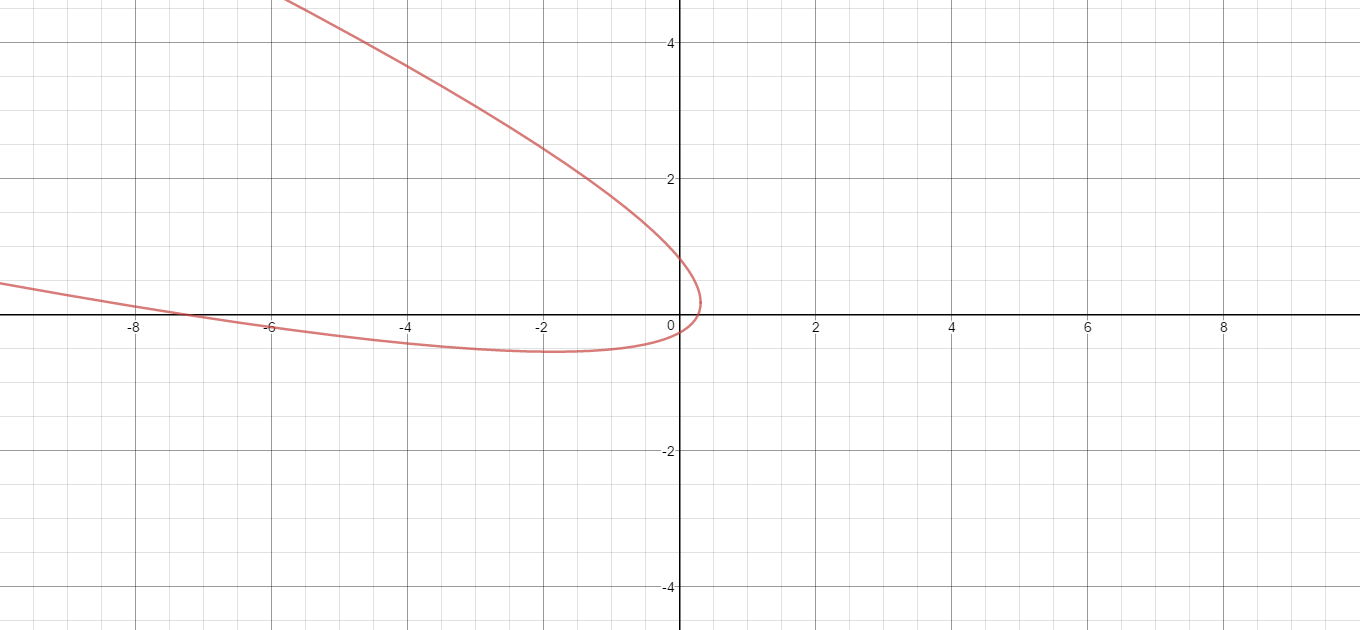
Given: #2=(-x-3y)^2-5y+7x#

Here is the graph of the Cartesian equation.

Desmos.com

Substitute #rcos(theta)# for x and #rsin(theta)# for y:

#2=(-rcos(theta)-3rsin(theta))^2-5rsin(theta)+7rcos(theta)#

Simplify:

#2=((-1)(r)(cos(theta)+3sin(theta)))^2+7rcos(theta)-5rsin(theta)#

#2=(-1)^2(r)^2(cos(theta)+3sin(theta))^2+(7cos(theta)-5sin(theta))r#

#0=(cos(theta)+3sin(theta))^2(r)^2+(7cos(theta)-5sin(theta))r -2#

#0=(cos(theta)+3sin(theta))^2r^2+ (7cos(theta)-5sin(theta))r - 2#

The above is a quadratic where #a = (cos(theta)+3sin(theta))^2, b = 7cos(theta)-5sin(theta) and c = -2#

Using the positive root of the quadratic formula:

#r = (5sin(theta)-7cos(theta) + sqrt((7cos(theta)-5sin(theta))^2+8(cos(theta)+3sin(theta))^2))/(2(cos(theta)+3sin(theta))^2)#

This is the polar equation.

Here is the graph of the polar equation

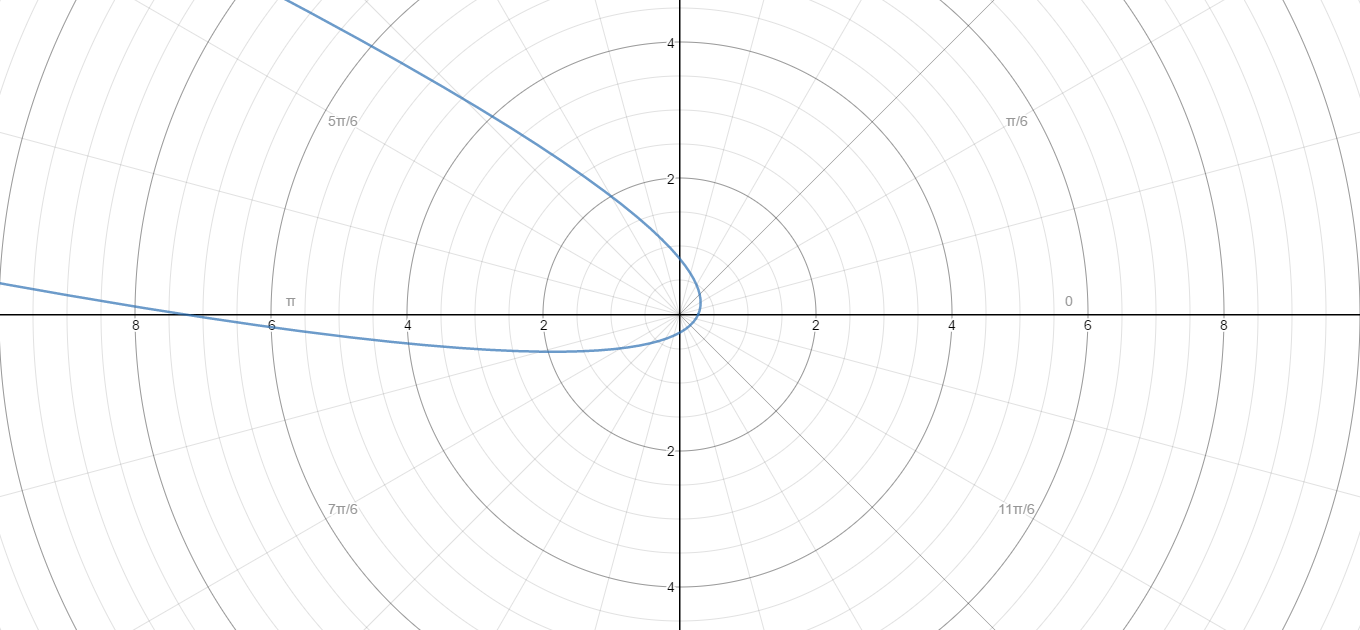
Desmos.com

This proves that the conversion is correct.