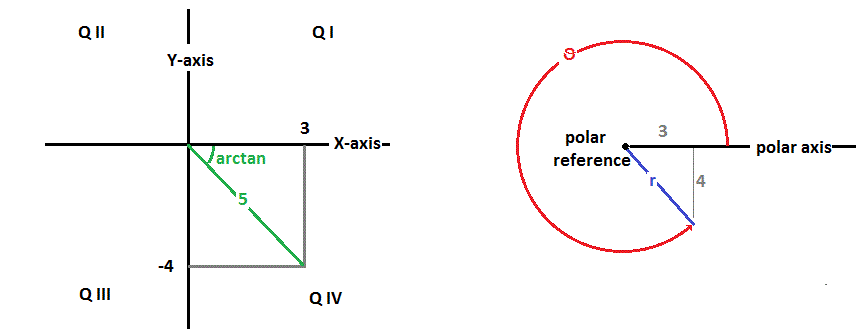
How do you convert #(3, - 4) # into polar coordinates?
1 Answer
Jan 4, 2016
Explanation:
The radius
The value of
#{: (color(black)("Quadrant"),,color(white)("XXX")color(black)(theta)), (bar(color(white)("XXXXXX")),,bar(color(white)("XXXXXX"))), (I,,arctan(y/x)), (II,,arctan(y/x)+pi), (III,,arctan(y/x)+pi), (IV,,arctan(y/x)+2pi) :}#