Question

How do you convert `8=(3x-y)^2+2y+6x` into polar form?

Answer 1

Please see the explanation.

Explanation:

Given: `8=(3x-y)^2+2y+6x`

Here is a graph of the Cartesian equation:
![Desmos.com]()

Expand the square:

`9x^2-6xy+y^2+6x+2y-8 = 0`

Substitute `rcos(theta)` for every x:

`9(rcos(theta))^2-6(rcos(theta))y+y^2+6(rcos(theta))+2y-8 = 0`

Substitute `rsin(theta)` for every y:

`9(rcos(theta))^2-6(rcos(theta))(rsin(theta))+(rsin(theta))^2+6(rcos(theta))+2(rsin(theta))-8 = 0`

There is a common factor of `r^2` in the first 3 terms:

`(9cos^2(theta)-6cos(theta)sin(theta)+sin^2(theta))r^2+6(rcos(theta))+2(rsin(theta))-8 = 0`

There is a common factor of r in the next 2 terms:

`(9cos^2(theta)-6cos(theta)sin(theta)+sin^2(theta))r^2+(6cos(theta)+2sin(theta))r-8 = 0`

The above is a quadratic equation in standard form where:

r in the independent variable

`a = 9cos^2(theta)-6cos(theta)sin(theta)+sin^2(theta)`

`b = 6cos(theta)+2sin(theta)`

`c = -8`

We use the identity #cos^2(theta) + sin^2(theta) = 1 to simplify a:

`a = 8cos^2(theta)-6cos(theta)sin(theta)+1`

We can use the quadratic formula to write r and a function of `theta` but, because radii should only be positive we will discard the negative root:

`r = (-b+sqrt(b^2-4(a)(c)))/(2a)`

Substitute for every a:

`r = (-b+sqrt(b^2-4(8cos^2(theta)-6cos(theta)sin(theta)+1)(c)))/(2(8cos^2(theta)-6cos(theta)sin(theta)+1))`

Substitute for c:

`r = (-b+sqrt(b^2+32(8cos^2(theta)-6cos(theta)sin(theta)+1)))/(2(8cos^2(theta)-6cos(theta)sin(theta)+1))`

Substitute for every b:

`r = (-(6cos(theta)+2sin(theta))+sqrt((6cos(theta)+2sin(theta))^2+32(8cos^2(theta)-6cos(theta)sin(theta)+1)))/(2(8cos^2(theta)-6cos(theta)sin(theta)+1))`

Here is a graph of the polar equation:

![Desmos.com]()

The graphs are identical, therefore, the conversion is complete.

Note: I am sure that the expression under the radical can be simplified but I will leave that to you.
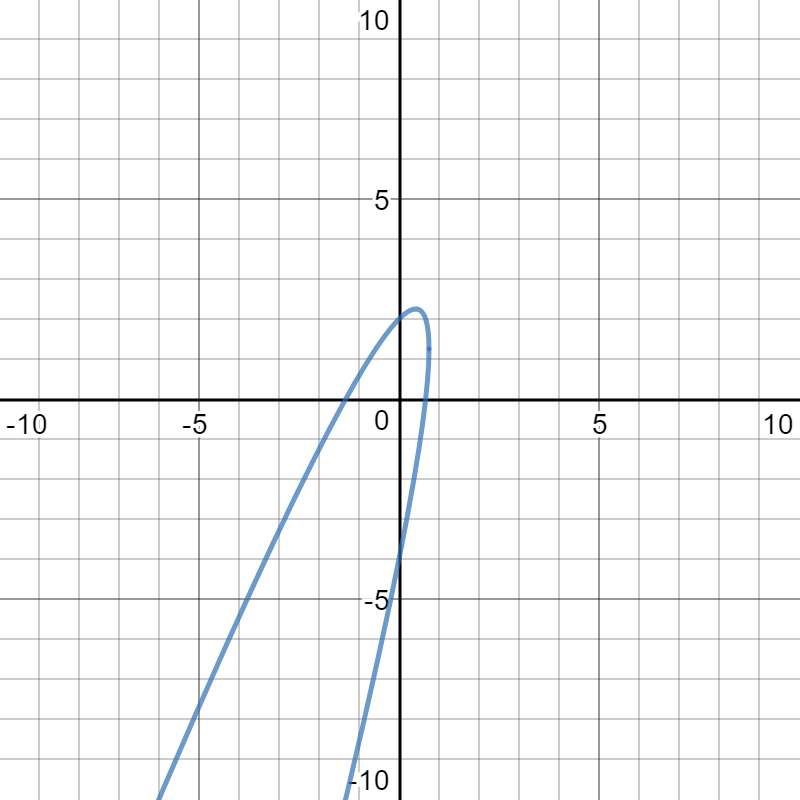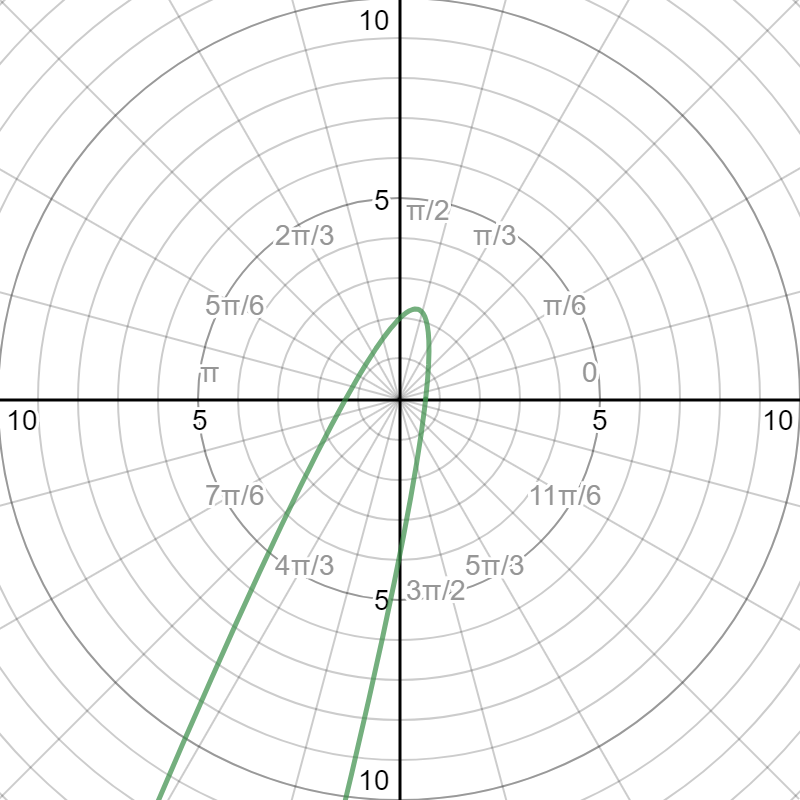