How do you convert polar equations to rectangular equations?
1 Answer
To convert an equation given in polar form (in the variables
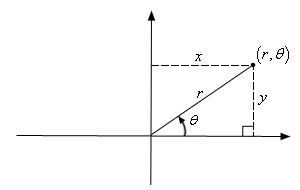
You have to remember that your equation may need some algebraic/trigonometric manipulations before being transformed into rectangular form; for example, consider:
Now you use the above transformations, and get:
Which is the equation of a straight line!
A more complicated situation can be the following example:
You can write:
Take the tangent of both sides and multiply and divide by
Transforming you get:

