Converting Equations from Polar to Rectangular
Key Questions
-
Answer:
See explanation
Explanation:
Imagine an arm where one end is pinned at the centre of a circular style graph and at the other end is a pencil. Also, the length of this arm can change such that its length is governed by a formula involving the angle of rotation.
Suppose the length of the arm is
#r# and we had one equation that was#r=5sintheta# and a second where#r=5sin(3theta)# Then we would have:
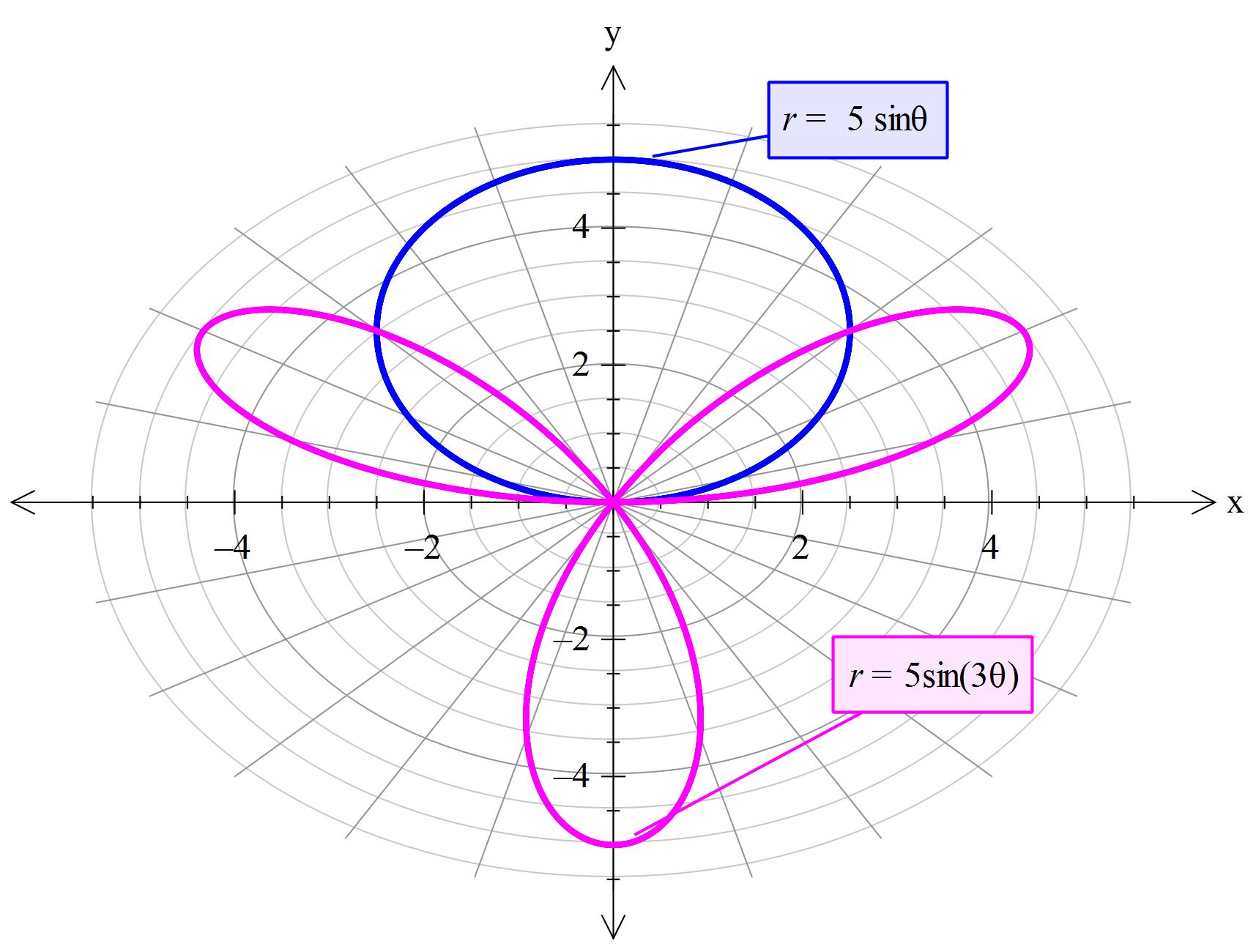
If you so chose you could graph it on standard graph paper. In which case it would look like:
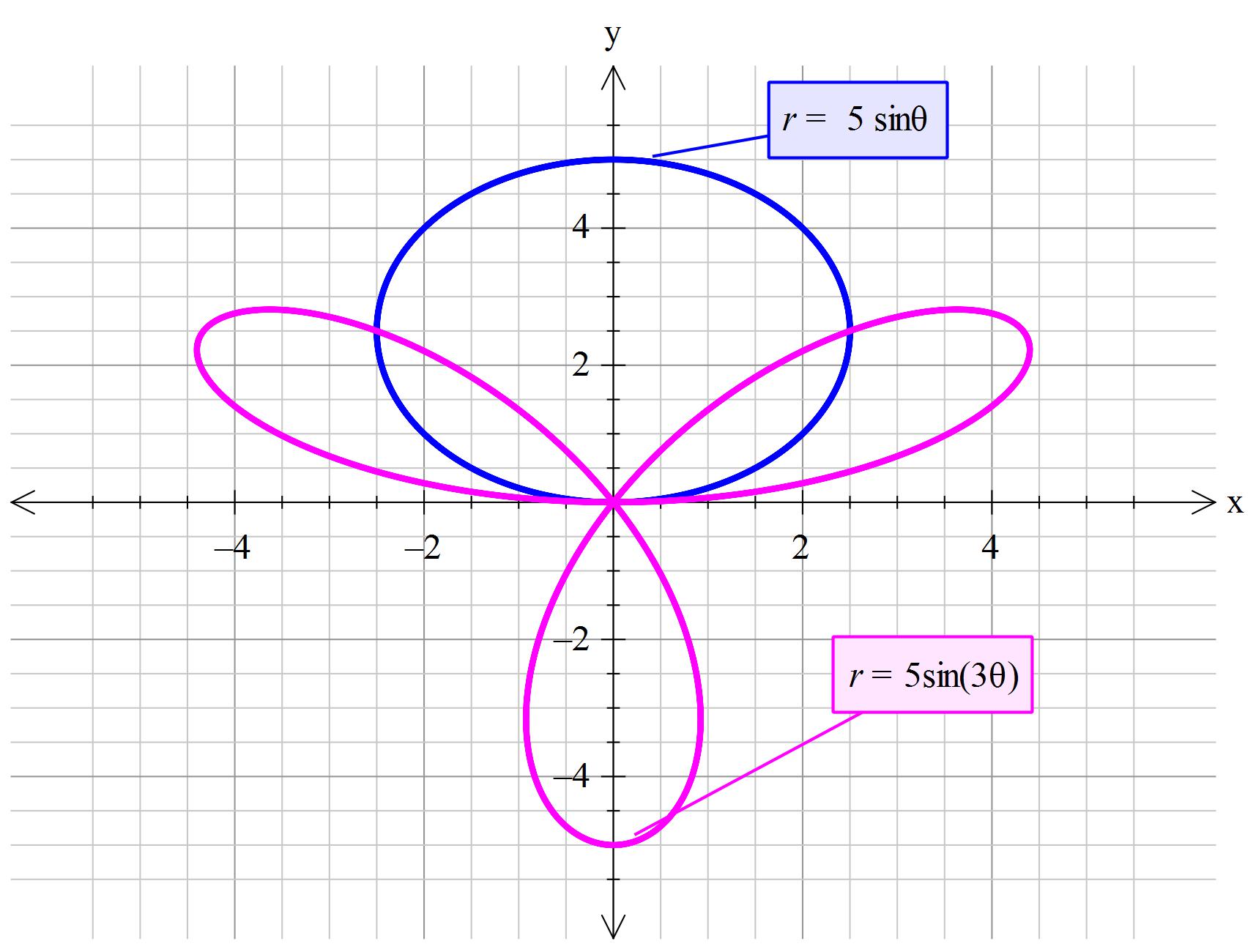
-
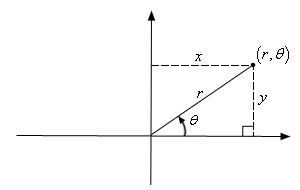
To convert an equation given in polar form (in the variables
#r# and#theta# ) into rectangular form (in#x# and#y# ) you use the transformation relationships between the two sets of coordinates:
#x=r*cos(theta)#
#y=r*sin(theta)#
You have to remember that your equation may need some algebraic/trigonometric manipulations before being transformed into rectangular form; for example, consider:#r[-2sin(theta)+3cos(theta)]=2#
#-2rsin(theta)+3rcos(theta)=2# Now you use the above transformations, and get:
#-2y+3x=2#
Which is the equation of a straight line!A more complicated situation can be the following example:
#theta+pi/4=0#
You can write:
#theta=-pi/4#
Take the tangent of both sides and multiply and divide by#r# the left side:
#r/r*tan(theta)=tan(-pi/4)#
#(rsin(theta))/(rcos(theta))=-1#
Transforming you get:
#y/x=-1#
#y=-x# -
Answer:
As discussed below.
Explanation:
Polar coordinates are a complementary system to Cartesian coordinates, which are located by moving across an x-axis and up and down the y-axis in a rectangular fashion. While Cartesian coordinates are written as (x,y), polar coordinates are written as (r,θ).
In polar coordinates, a point in the plane is determined by its distance r from the origin and the angle theta (in radians) between the line from the origin to the point and the x-axis
The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction
Why is it called Polar form?
In polar coordinates the origin is often called the pole. Because we aren't actually moving away from the origin/pole we know that . However, we can still rotate around the system by any angle we want and so the coordinates of the origin/pole are .Who invented polar coordinates?
The polar coordinate system is an adaptation of the two-dimensional coordinate system invented in 1637 by French mathematician René Descartes (1596–1650). Several decades after Descartes published his two dimensional coordinate system, Sir Isaac Newton (1640–1727) developed ten different coordinate systems.Is it helpful?