Question

How do you convert `r= 2cos theta` to rectangular form?

Answer 1

Rectangular Form `color(purple)((x-1)^2 + y^2 = 1`

Explanation:

Given : `r = 2 cos theta`

![enter image source here]
()

()

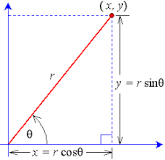From the diagram above,
`y = r sin theta, x = r cos theta`

But given `r = 2 cos theta`

`:. r ^2 = 2 r cos theta color(white)aaa)` Multiplying both sides by `r`

`r^2 = 2 * r cos theta = 2 x`

But `x^2 + y^2 = r^2`

Hence, x^2 + y^2 = 2x#

`x^2 - 2x + y^2 = 0`

![https://www.slideshare.net/jessicagarcia62/64-solve-quadratic-equations-by-completing-the-square]()
`x^2 - 2x + 1 + y^2 = 1 color(white)(aaa)` Adding 1 to both sides to complete the square.

`color(purple)((x-1)^2 + y^2 = 1`