How do you convert #-xy=-x^2+4y^2 # into a polar equation?

Question

1377 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-03-15T00:04:22

Substitute:

#x=rcosθ#
#y=rsinθ#

Polar equation is

#-rcosθ*rsinθ=-(rcosθ)^2+4(rsinθ)^2#

or, with some trigonometric identities:

#10sin^2θ+sin2θ-2=0#

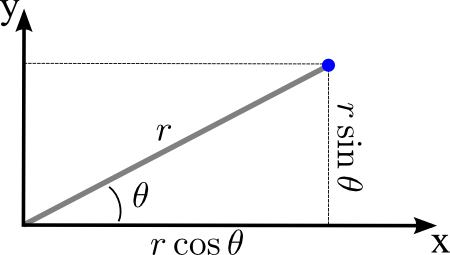
mathinsight.org

Therefore:

#x=rcosθ#

#y=rsinθ#

So, by substituting:

#-xy=-x^2+4y^2#

#-rcosθ*rsinθ=-(rcosθ)^2+4(rsinθ)^2#

#-r^2cosθsinθ=-r^2cos^2θ+4r^2sin^2θ#

Divide by #r^2# since #r>0#

#-cosθsinθ=-cos^2θ+4sin^2θ#

Using trigonometric identities:

#sin2θ=2sinθcosθ#

#sin^2θ+cos^2θ=1#

We have:

#-(sin2θ)/2=-(1-sin^2θ)+4sin^2θ#

#-(sin2θ)/2=-1+sin^2θ+4sin^2θ#

#-(sin2θ)/2=5sin^2θ-1#

#10sin^2θ+sin2θ-2=0#