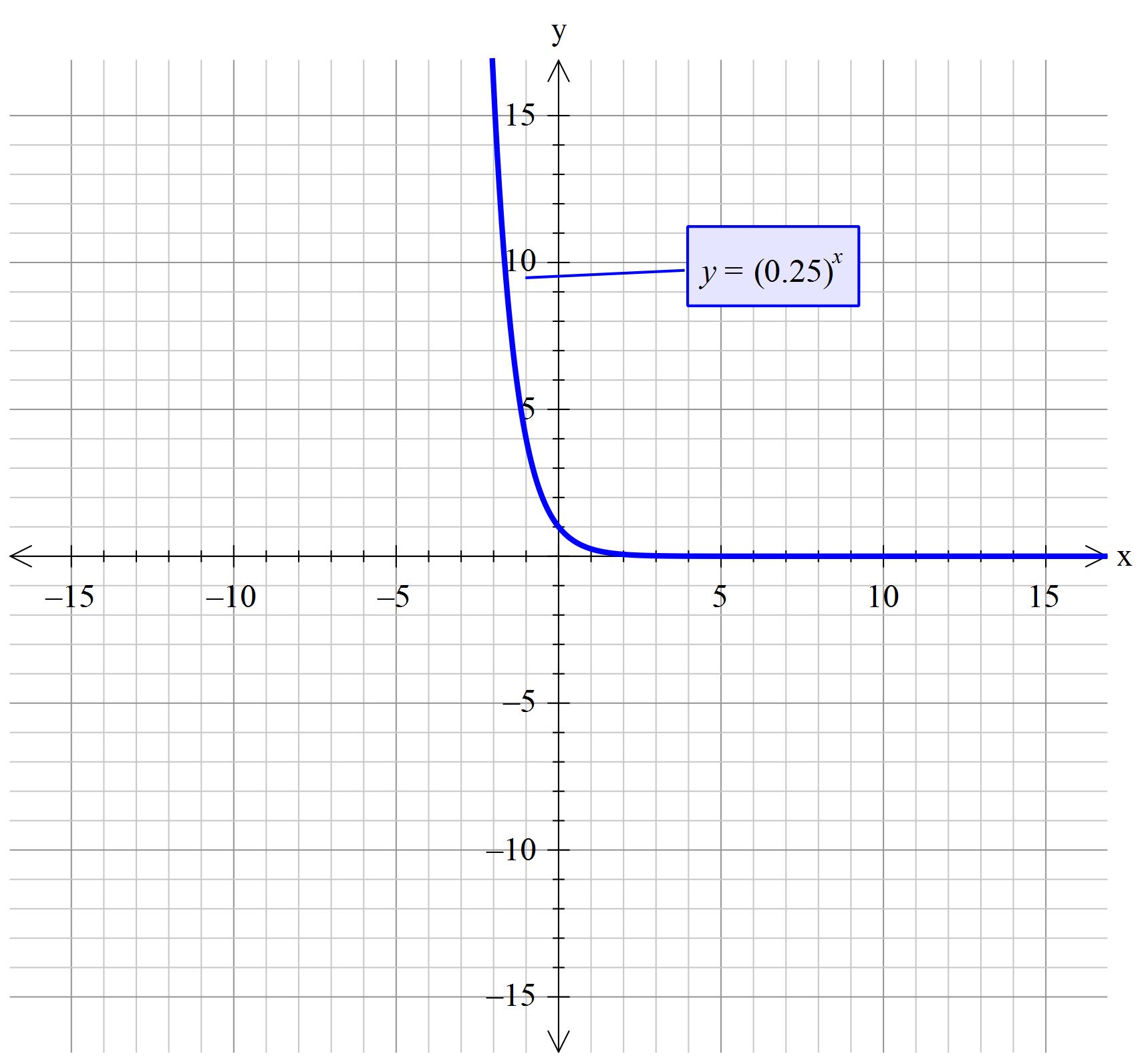
#color(brown)("Suppose "x<0" then we have "y=1/(0.25^n))#
#color(magenta)(" "uarr)#
#color(magenta)(" ( only for negative "x")")#
Where #n=(-1)xx x#
As you read from left to right #n# becomes closer and closer to 0 so
#0.25^n# becomes bigger thus #1/0.25^n# becomes less
Think of #1/((1/2)^3)=1/(1/8)" but "1/((1/2)^2) =1/(1/4)#
so #1/((1/2)^3)" " >" " 1/((1/2)^2)#
#color(blue)("For "x < 0 " there is decay as "x" increases.")#
#-2" is more than "-3# as you are moving to the right on the number line.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Suppose "x>=0" then we have "y=(0.25)^x)#
At #x=0# we have #y=1/1=1#
At #x=0^+ y < 1# so there is decay
At #x > 0, (0.25)^x" becomes even less"#
#y=(0.25)^1 = 0.25#
#y=(0.25)^2= 1/4^2 = 1/16#
#y=(0.25)^2=1/4^3=1/64#
#color(blue)("For "x >=0" there is decay as "x" increases")#