How do you determine if the series the converges conditionally, absolutely or diverges given #Sigma ((-1)^(n))/(lnn)# from #[1,oo)#?
1 Answer
Dec 9, 2016
The series is convergent.
Explanation:
We have that
This series is converget if
1)
2)
This series accomplishes both requirements so it is convergent.
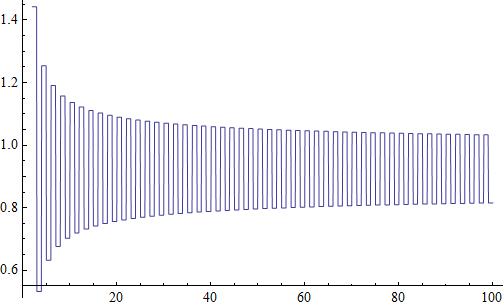
Attached a plot of