How do you determine the equation of the circle, given the following information: center = (8, 6), passing through (7, -5)?
1 Answer
You are going to use the equation of the circle and the Euclidian distance.
Explanation:
The equation of the circle is:
Where:
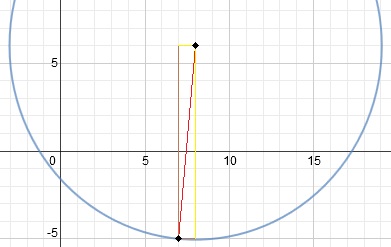
The radius is defined as the distance between the circle center and any point of the circle. The point that the circle is passing through can be used for this. The Euclidian distance can be calculated:
Where
Note: the order of numbers inside the powers doesn't matter.
Therefore, we can now substitutein the equation of the circle as follows:
Note: As shown in the next image, the Euclidian the distance between the two points is obviously calculated through the use of the Pythagorean theorem.
graph{(x-8)^2+(y-6)^2=122 [-22.2, 35.55, -7.93, 20.93]}
