How do you determine the exact coordinates of a point on the terminal arm of the angle in standard position given 45 degrees?
1 Answer
Feb 26, 2018
See below.
Explanation:
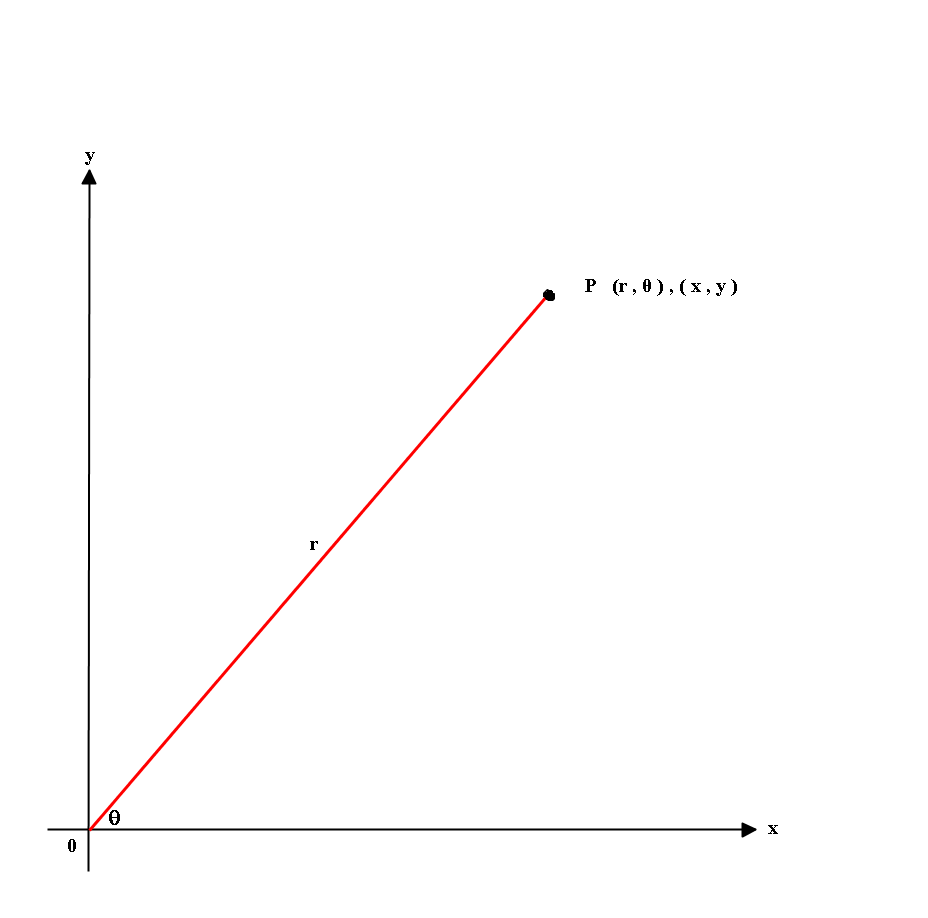
By looking at the diagram we can find a relationship between the Cartesian coordinates and the angular measurement.
Point
Where
So using this idea:
For:
radius
So coordinates are:

