Question

How do you determine the quadrant in which the angle `-3.4^circ` lies?

Answer 1

IVth quadrant

Explanation:

It is quite simple. Because of the negative sign of the angle, move clockwise `3.4^o` from the `0^o`line. It stops in the IVth quadrant.

Answer 2

The angle `-3.4°` lies in quadrant 4 (`Q_"IV"`).

Explanation:

When we talk about the quadrant an angle is in, we're really talking about the quadrant the terminal arm of the angle is in, when the angle is drawn with its initial arm along the `+x` axis (a.k.a. standard position).

To draw an angle, imagine a clock centered at the origin, with the minute hand pointing to the right (at the "3"). Then, rotate the hand counterclockwise (towards the "12") by the amount of the angle. Since the angle `-3.4°` is negative, we end up rotating clockwise (towards the "6") by 3.4 degrees.

Now, `-3.4°` is quite small compared to a full `360°` circle, so we will only rotate a little bit (not even to the "4" on our clock). So we have our terminal arm in the bottom-right quadrant.

Which quadrant is this? The quadrants are named in increasing order, starting with quadrant 1 (`Q_"I"`) in the top right, and moving counterclockwise to `Q_"II"` in the top left, etc. In this way, higher numbered quadrants contain bigger angles (until `360°`, of course).

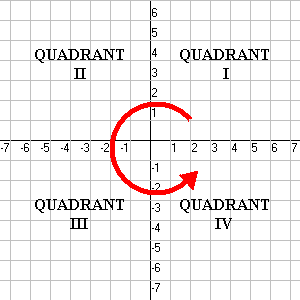
So the angle `-3.4°` lies in `Q_"IV"`.