How do you differentiate 4xy-3x-11=04xy−3x−11=0?
2 Answers
Explanation:
Assume the equation
Now solve for
If you happen to know a specific point
The particular equation
Now we can differentiate this in the ordinary way to get
It is the same!
As an example of a point on this curve, we can use the equation
The equation of the tangent line to the curve at that point is therefore
Here's a graph of the situation just described:
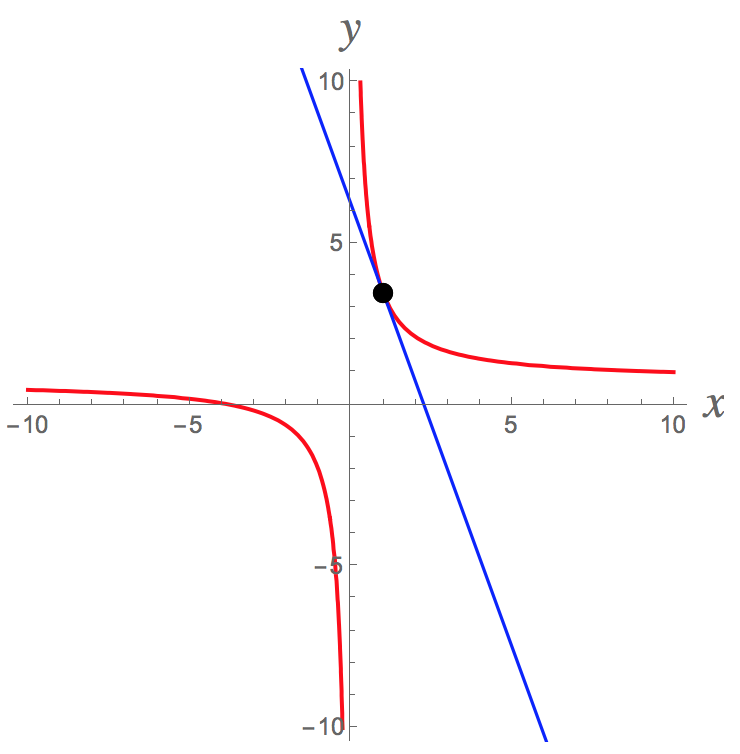
Assuming that we want to find
Using implicit differentiation, we get:
Solving for
Explanation:
The question is posted under "Implicit Differentiation", so let's do it that way first:
Leaving the function Implicit
In order to differentiate
Remember that we are assuming that
the derivative is:
Back to this problem:
Making the function explicit
Solve
We could differentiate using the quotient rule, but it is perhaps simpler to rewrite again:
= 3/4 +11/4x^-1
So
= -11/(4x^2)
The answers are equivalent
To see that the answer are equivalent compare:
with
Using Implicit differentiation, there is still a
= (3-(3x+11)/x)/(4x)
= (3x-3x-11)/(4x^2)
= -11/(4x^2)


