Start by making the assumption that this equation "implicitly defines" #y# as a function of #x# (more on this later). Once you've made this assumption, then differentiate both sides of the equation with respect to #x#, using the Chain Rule and Product Rule, to get:
#e^{y} * dy/dx * cos(x)-e^{y} * sin(x)=cos(xy) * (x * dy/dx+y)#
(If you prefer, you could write this as: #e^{f(x)}f'(x)cos(x)-e^{f(x)}sin(x)=cos(x f(x))(x f'(x)+f(x))# )
This equation, complicated as it looks, can be solved for #dy/dx#. First, use the distributive property on the right-hand side to get:
#e^{y} dy/dx cos(x)-e^{y} sin(x)=x cos(xy) dy/dx+y cos(xy)#
Now get the terms involving #dy/dx# on one side and the other terms on the other side (and do a bit of factoring):
#(e^{y}cos(x)-x cos(xy)) dy/dx=y cos(xy)+e^{y}sin(x)#
Now divide both sides by #(e^{y}cos(x)-x cos(xy))# to get the final answer:
#dy/dx=(y cos(xy)+e^{y}sin(x))/(e^{y}cos(x)-x cos(xy))#
(alternatively, #f'(x)=(f(x) cos(x f(x))+e^{f(x)}sin(x))/(e^{f(x)}cos(x)-x cos(x f(x)))#)
But what does this mean? The original equation #e^{y}cos(x)=8+sin(xy)# cannot be "explicitly" solved for #y# as a function of #x#. However, if you use technology to make a graph of this equation, you will see that there are many pieces of this graph that pass the vertical line test, and therefore each of those pieces can be thought of as defining #y# as a function of #x# (avoid pieces where the vertical line test fails). This means the original equation defines #y# "implicitly" as a function of #x# on pieces that pass the vertical line test (essentially you want to avoid places where the tangent line is vertical).
I graphed this equation using ContourPlot on Mathematica (Wolfram Alpha gave me trouble with it) and got the following picture, which seems to pass the vertical line test when #x# is close to zero but have "more difficulty" passing it as #x# gets further from zero (pieces will still pass it though).
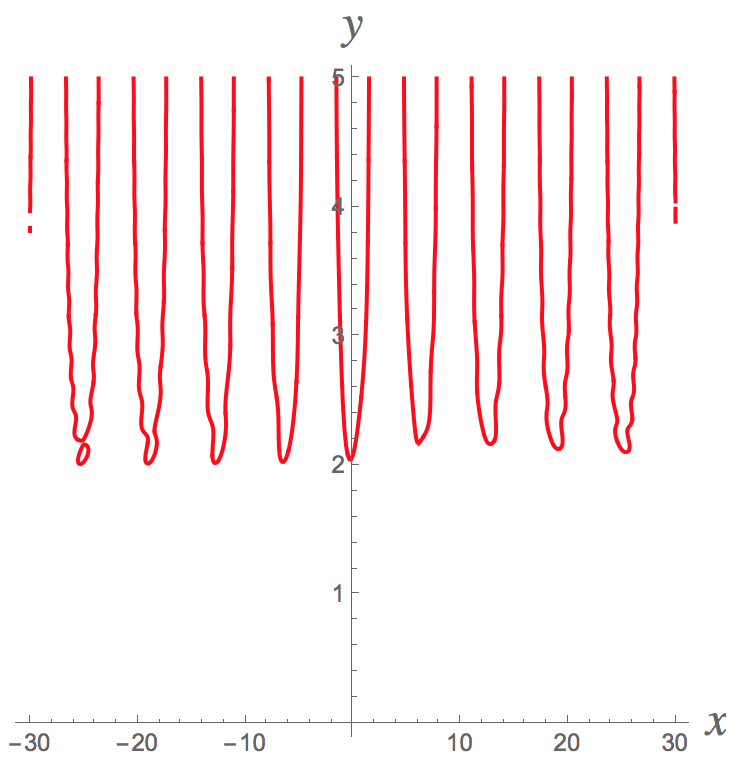
The derivative we found, #dy/dx=(y cos(xy)+e^{y}sin(x))/(e^{y}cos(x)-x cos(xy))#, will give you slopes of tangent lines at known points #(x,y)# on exactly on the graph above.
What's an example of a known point? The simplest one I could think of is #(x,y)=(0,ln(8))\approx (0,2.08)# (go back to the original equation to see this). The slope at this point is therefore
#dy/dx=(ln(8)cos(0)+e^{ln(8)}sin(0))/(e^{ln(8)}cos(0)-0*cos(0))=ln(8)/8\approx 0.26#


