Question

How do you differentiate `f(x)=x/(x-4)^2` using the quotient rule?

Answer 1

See below.

Explanation:

The quotient rule is given by

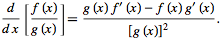
In this case, `f(x)=x` and `g(x)=(x-4)^2`. We will also make use of the chain rule.

As indicated, we will first take the derivative of `f(x)` and multiply this by `g(x)`, which we leave as is.

`f'(x)=1`

`g(x)f'(x)=(x-4)^2`

From this, we subtract the product of `g'(x)` and `f(x)`, which we leave as is. We will use the chain rule to differentiate `g(x)`.

`g'(x)=2(x-4)(1)`

`f(x)g'(x)=2x(x-4)`

And, `[g(x)]^2` is `[(x-4)^2]^2=(x-4)^4`

The derivative is then given as:

`f'(x)=((x-4)^2-2x(x-4))/(x-4)^4`

Which simplifies to

`((x-4)-2x)/(x-4)^3`

`=>(-x-4)/(x-4)^3`

`=>f'(x)=-(x+4)/(x-4)^3`