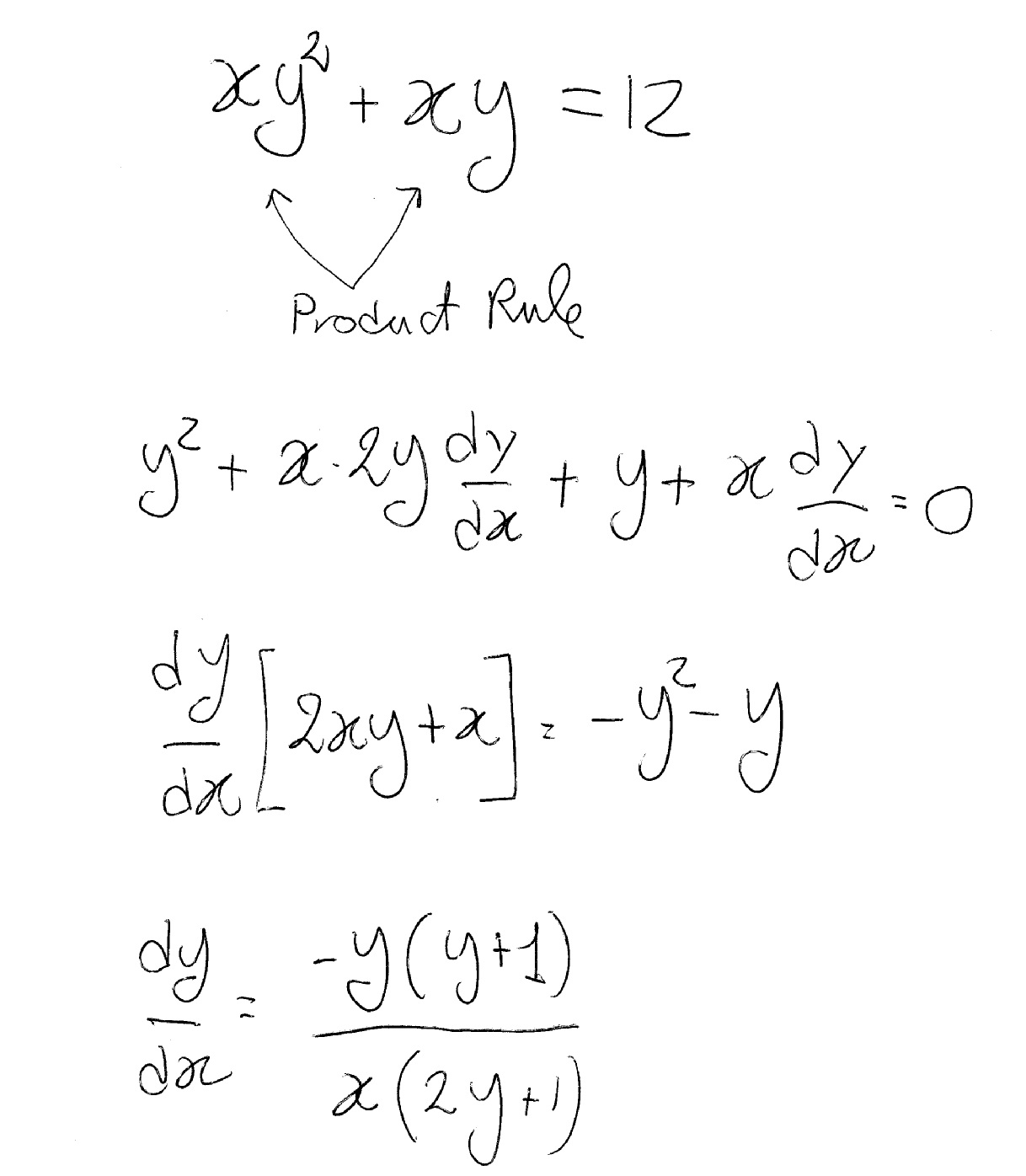You start by assuming the equation defines yy as a function of xx (the method we're about to use is called "implicit differentiation" because yy has not been solved for explicitly in terms of xx). Then you differentiate both sides with respect to xx, using the Product Rule and Chain Rule to get the following (using Lebniz notation):
y^2+2xy\frac{dy}{dx}+y+x\frac{dy}{dx}=0.y2+2xydydx+y+xdydx=0.
This is an algebra equation that you can now solve for the derivative dy/dxdydx to get:
\frac{dy}{dx}=\frac{-y^{2}-y}{2xy+x}.dydx=−y2−y2xy+x.
If this is confusing, it might be less confusing if you write y=f(x)y=f(x) and then write the original equation as x(f(x))^2+xf(x)=12x(f(x))2+xf(x)=12. Now when you differentiate both sides with respect to xx, you'd write the initial result as
(f(x))^2+2xf(x)f'(x)+f(x)+xf'(x)=0
and then solve for f'(x) to get
f'(x)=\frac{-(f(x))^2-f(x)}{2xf(x)+x}.
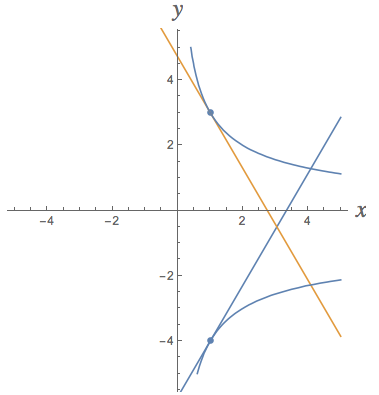
To use this derivative to find the slope of the curve at a specific value of x, you'd also have to find a corresponding value of y and plug both numbers into the equation for the derivative. For example, if x=1, then the original equation becomes y^2+y=12 or y^2+y-12=0 or (y+4)(y-3)=0, giving two corresponding values of y: y=-4 and y=3.
The slope of the curve at (x,y)=(1,-4) would be \frac{dy}{dx}=\frac{-(-4)^2-(-4)}{2\cdot 1\cdot (-4)+1}=\frac{-12}{-7}=\frac{12}{7} and the slope of the curve at (x,y)=(1,3) would be \frac{dy}{dx}=\frac{-(3)^2-(3)}{2\cdot 1\cdot (3)+1}=\frac{-12}{7}=-\frac{12}{7}.
Here's a picture of this situation: