How do you differentiate #y=arcsin(x)#?

I don't even know where to start.

I watched a video on You Tube of how to do it, but it just didn't make any sense to me. Hope someone can help.

Thanks

3 Answers
Somebody N.
Jan 17, 2018

See below.

Explanation:

#y=arcsin(x)#

Before we proceed we need to understand just what it is we are looking for. Remember that:

#y=arcsin(x)# is the inverse function of #y=sin(x)#

This can be expressed as:

#y=arcsin(x) <=> x=sin(y)#

Using

#x=sin(y)#

We need to differentiate in respect of #x#, so this will need to be differentiated implicitly.

Remembering that:

#d/dx(f(y))= (d)/(dy)(f(y))*dy/dx#

#dy/dx(x)=d/(dy)(sin(y))*dy/dx#

#1=cos(y)*dy/dx#

#dy/dx=1/cos(y)#

From above #y = arcsin(x)#

Substitutng in #dy/dx=1/cos(y)#

#:.#

#dy/dx=1/cos(arcsin(x))#

This is a little awkward, and it would be easier if we could express this in a different way.

Using the Pythagorean identity:

#color(red)(sin^2(y)+cos^2(y)=1)#

#cos(y)=+-sqrt(1-sin^2(y))#

Using positive root: ( see below)

#:.#

#dy/dx=1/(sqrt(1-sin^2(y)))#

From above #x=sin(y)#

Hence:

#dy/dx=1/(sqrt(1-x^2)#

#:.#

#dy/dx(arcsin(x))=1/(sqrt(1-x^2)#

Reason for using positive root of #sqrt(1-sin^2(y))#

This is because #y=sin(x)# only has an inverse if we restrict the domain to:

#-pi/2 <= x <= pi/2#

In #color(white)(88)1/cos(y)# , #color(white)(88)y# is an angle and it is an angle in the range

#-pi/2 <= x <= pi/2#

This range is in the I and IV quadrants, where the cosine ratios are positive.

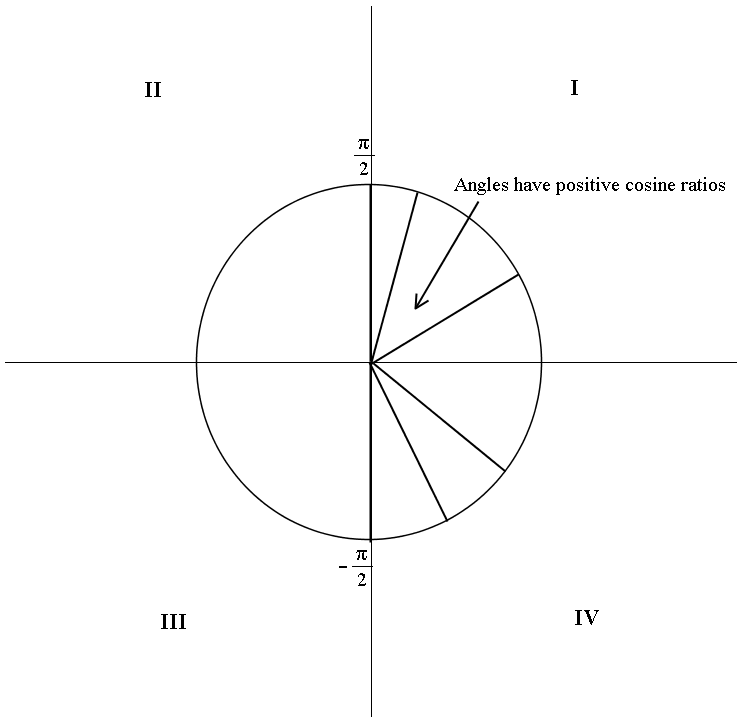
enter image source here

Anthony R.
Jan 17, 2018

Here's an alternative solution

Explanation:

This troubled me as well when I was first learning these kinds of derivatives. Here's how I learned how to tackle this type of problem:

Similarly to what was said below, #y=arcsin(x)# is just the inverse of #y=sin(x)#

When trying to take the derivative of #y=arcsin(x)# we can rewrite this as:

#color(blue)(sin(y)=x#

It is at this point where I would create a right triangle showing this

Recall: #sin(y)="Opposite"/"Hypothenuse"#

In this case #sin(y)=x/1#

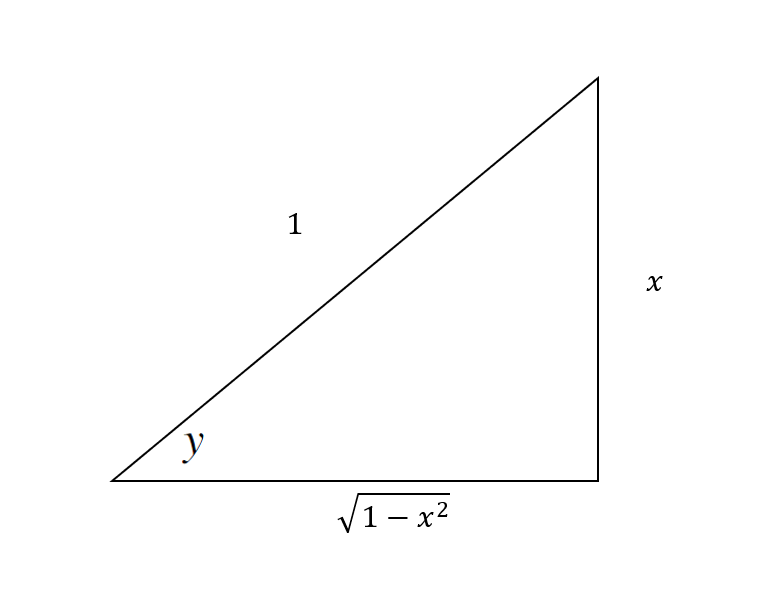
enter image source here

We can solve for the missing side using #a^2+b^2=c^2# which will give you #sqrt(1-x^2)#. This will be useful later!

Now we'll differentiate implicitly (W.R.T #x#):

#dy/dx*cos(y)=1#

Divide #cos(y)# from both sides

#dy/dx=1/cos(y)#

Now we'll have to rewrite in terms of #x# but you may notice that we #color(red)(cos(y))# in the way but what is #color(red)(cos(y)#?

Well based on the triangle we made above:

#cos(y)="Adjacent"/"Hypothenuse"#

#color(red)(cos(y)=sqrt(1-x^2)/1=sqrt(1-x^2)#

So #dy/dx=1/cos(y)=1/sqrt(1-x^2)#

#:.dy/dx[arcsin(x)]=1/sqrt(1-x^2)#

The neat thing about this is that this is useful for the other inverse functions like #y=arccos(x)#

#y=arccos(x)<=>cos(y)=x#

Create a triangle:

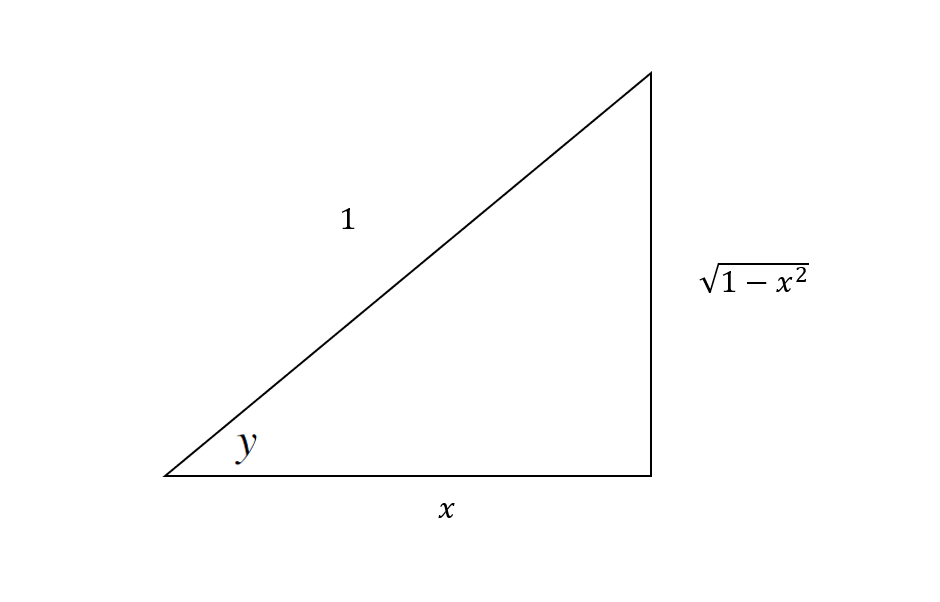
enter image source here

Differentiate both sides implicitly (W.R.T #x#)

#dy/dx*-sin(y)=1#

Divide both sides by #-sin(y)#

#dy/dx=-1/sin(y)#

Rewrite in terms of #x#

Since #cos(y)=x/1#

Then #sin(y)=sqrt(1-x^2)/1=sqrt(1-x^2)#

So #dy/dx=-1/sin(y)=-1/sqrt(1-x^2)#

#:.dy/dx[arccos(x)]=-1/sqrt(1-x^2)#

Also if you have something like #y=arcsin(3x)# the same process applies but the triangle will be different based on whatever the coefficient is.

So...

#y=arcsin(3x)<=>sin(y)=3x#

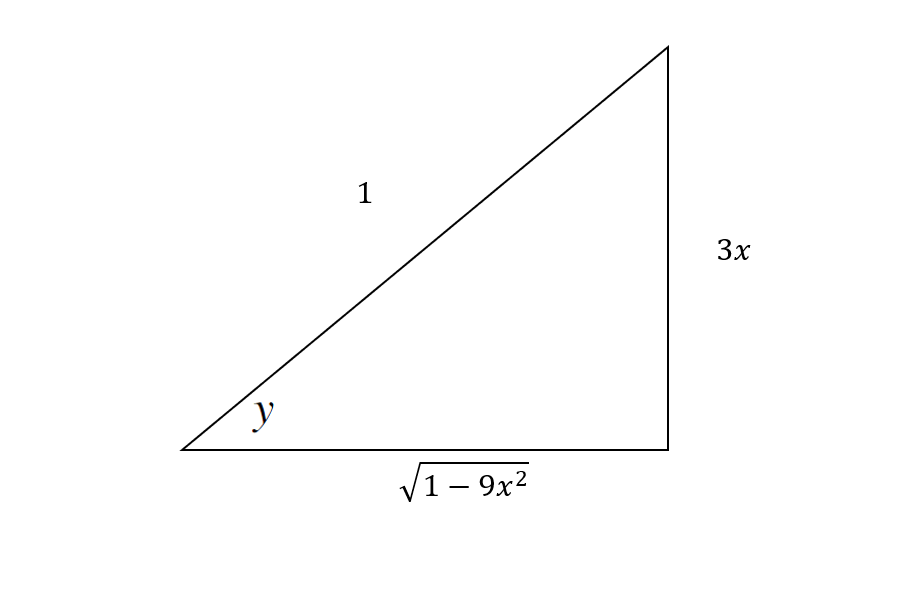
enter image source here

Differentiate implicitly (W.R.T #x#):

#dy/dx*cos(y)=3#

#dy/dx=3/cos(y)#

Since #sin(y)=(3x)/1#

Then #cos(y)=sqrt(1-9x^2)/1=sqrt(1-9x^2)#

So #dy/dx=3/cos(y)=3/sqrt(1-9x^2)#

#:.dy/dx[arcsin(3x)]=3/sqrt(1-9x^2)#

I hope I explained this well!

Monzur R.
Jan 17, 2018

#dy/dx = 1/cos(arcsinx)=1/sqrt(1-x^2)dx#

Explanation:

There is another way to do it. We have a formula for calculating the derivatives of inverse functions:

#(f^-1)^'(x)=1/(f^'(f^-1(x))#

Here #f^-1(x)=arcsinx rArr f(x)=sinx# and #f^'(x)=cosx#

So #(arcsinx)^'=1/cos(arcsinx)#

Using the arguments given in the other answers, we know that

#1/cos (arcsinx)=1/sqrt(1-x^2)#

Related questions
Impact of this question
31929 views around the world
You can reuse this answer
Creative Commons License