How do you differentiate #y=arcsin(x)#?
I don't even know where to start.
I watched a video on You Tube of how to do it, but it just didn't make any sense to me. Hope someone can help.
Thanks
I don't even know where to start.
I watched a video on You Tube of how to do it, but it just didn't make any sense to me. Hope someone can help.
Thanks
3 Answers
See below.
Explanation:
Before we proceed we need to understand just what it is we are looking for. Remember that:
This can be expressed as:
Using
We need to differentiate in respect of
Remembering that:
From above
Substitutng in
This is a little awkward, and it would be easier if we could express this in a different way.
Using the Pythagorean identity:
Using positive root: ( see below)
From above
Hence:
Reason for using positive root of
This is because
In
This range is in the I and IV quadrants, where the cosine ratios are positive.
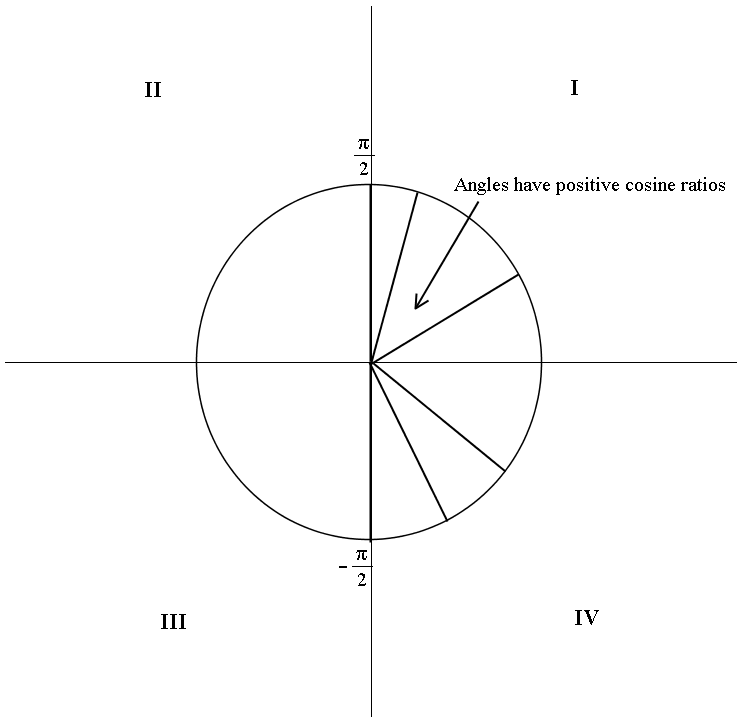
Here's an alternative solution
Explanation:
This troubled me as well when I was first learning these kinds of derivatives. Here's how I learned how to tackle this type of problem:
Similarly to what was said below,
When trying to take the derivative of
It is at this point where I would create a right triangle showing this
Recall:
In this case
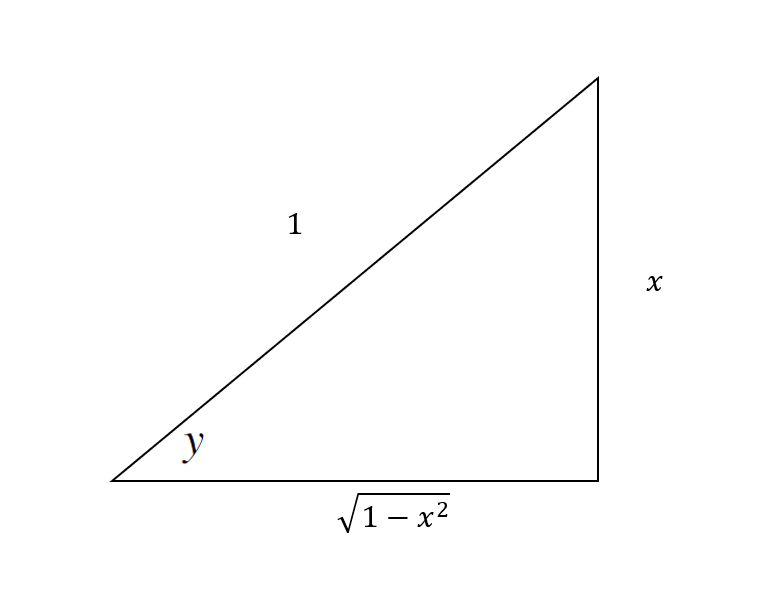
We can solve for the missing side using
Now we'll differentiate implicitly (W.R.T
Divide
Now we'll have to rewrite in terms of
Well based on the triangle we made above:
So
The neat thing about this is that this is useful for the other inverse functions like
Create a triangle:
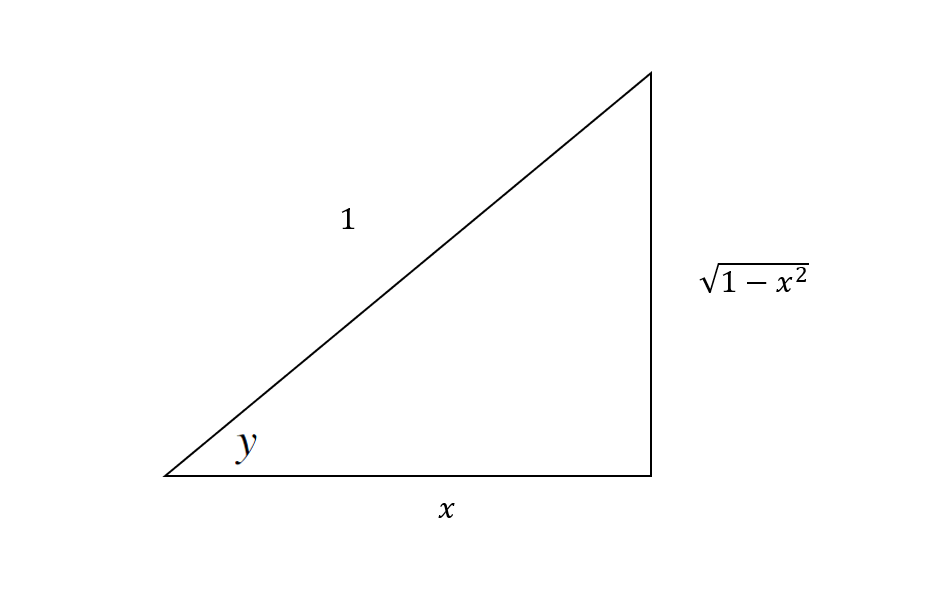
Differentiate both sides implicitly (W.R.T
Divide both sides by
Rewrite in terms of
Since
Then
So
Also if you have something like
So...
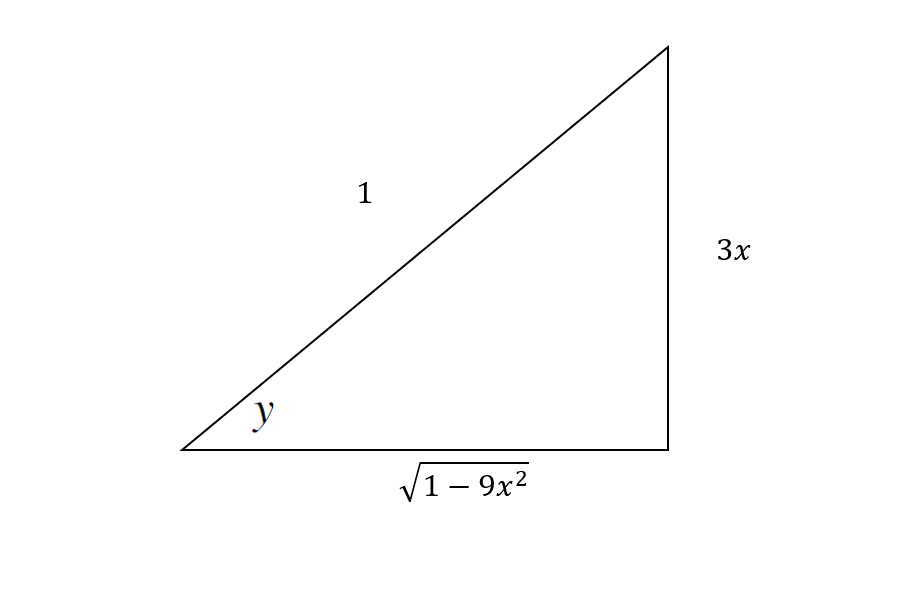
Differentiate implicitly (W.R.T
Since
Then
So
I hope I explained this well!
Explanation:
There is another way to do it. We have a formula for calculating the derivatives of inverse functions:
Here
So
Using the arguments given in the other answers, we know that



