How do you differentiate #y=sin(xy)#?
2 Answers
Jun 17, 2015
Explanation:
Assuming you are differentiating with respect to
No rearrange this equation as
Since the original equation cannot be solved explicitly for
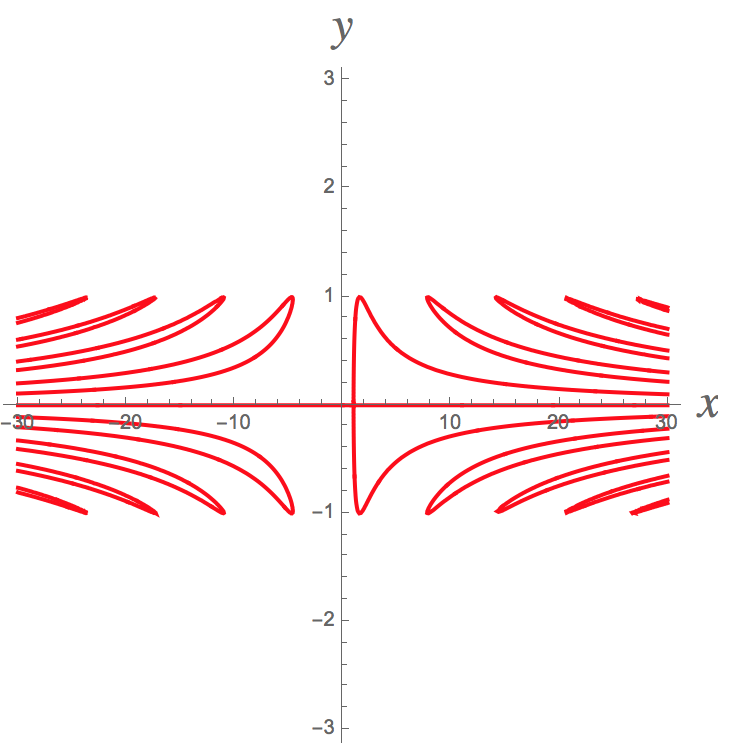
Nov 4, 2017
BTW, the graph of this equation is very beautiful
Explanation:
Here's the graph: