How do you divide #(x^5 + x^3 − 9)/(x-1) #?

1 Answer
George C.
Mar 7, 2016

#(x^5+x^3-9)/(x-1) = (x^4+x^3+2x^2+2x+2)-7/(x-1)#

Explanation:

You can long divide the coefficients, not forgetting to include #0#'s for any missing powers of #x# ...

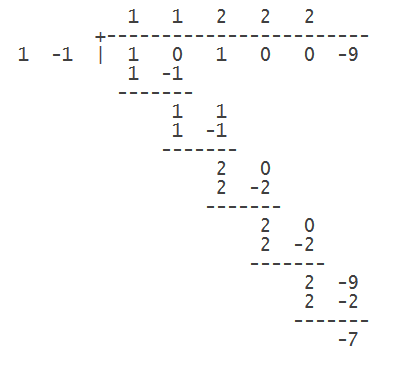
enter image source here

In our example we find:

#x^5+x^3-9 = (x-1)(x^4+x^3+2x^2+2x+2)-7#

or if you prefer:

#(x^5+x^3-9)/(x-1) = (x^4+x^3+2x^2+2x+2)-7/(x-1)#

That is: #(x^5+x^3-9)# divided by #(x-1)# is #(x^4+x^3+2x^2+2x+2)# with remainder #-7#.

If all we wanted to know was the remainder, then we could have substituted #x=1# into #x^5+x^3-9# to get #1+1-9 = -7#

Alternative Method

Alternatively, start writing out the answer linearly, evaluating the partial sums as you go along and choosing the next term accordingly:

#x^5+x^3-9#

#(x-1)(x^4 color(white)(xxxxxxxxxxxxxxx)# gives #x^5-x^4#

#(x-1)(x^4+x^3 color(white)(xxxxxxxxxxx)# gives #x^5-x^3#

#(x-1)(x^4+x^3+2x^2 color(white)(xxxxxxx)# gives #x^5+x^3-2x^2#

#(x-1)(x^4+x^3+2x^2+2x color(white)(xxxx)# gives #x^5+x^3-2x#

#(x-1)(x^4+x^3+2x^2+2x+2) color(white)(x)# gives #x^5+x^3-2#

#(x-1)(x^4+x^3+2x^2+2x+2) -7 color(white)(x)# gives #x^5+x^3-9#

Related questions
See all questions in Long Division of Polynomials
Impact of this question
1374 views around the world
You can reuse this answer
Creative Commons License