Question

How do you draw a box and whisker plot of the data: 29, 33, 36, 37, 39, 40, 41?

Answer 1

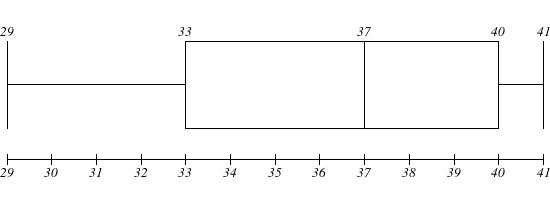
Explanation:

`29, 33, 36, 37, 39, 40, 41`

The minimum is the lowest number in the data set.
Since it is listed from smallest to largest, we know that the minimum is `29`.
``

The median is the middle number. Cancel out `3` numbers from each side and we are left with the median:
`cancel(29), cancel(33), cancel(36), 37, cancel(39), cancel(40), cancel(41)`

Therefore, the median is `37`.

The first quartile (Q1) is the median of the lower half of data which lies at 25% of the data.
Let's look at the lower half of numbers:
`29, 33, 36`

The number in the middle is `33`, so that is the first quartile.

The third quartile (Q3) is the median of the upper half of data which lies at 75% of the data.

Let's look at the upper half of numbers:
`39, 40, 41`

The number in the middle is `40`, so that is the third quartile.

The maximum is the highest number in the data set; it is `41`.

So here's the five-number summary:
Minimum: 29

First quartile: 33

Median: 37

Third quartile: 40

Maximum: 41

This is what a typical box-and-whisker plot looks like:

So here's the box-and-whisker plot for this data:

Hope this helps!