I'm not sure if this long answer is going to satisfy your request or not. If you are interested in more advanced analytical ways to get the behavior of solutions of differential equations, please let me know in the comments.
In this answer I consider the computational approach, which I find easier to introduce in this context.
The slope field of #dy/dx=f(x,y)# is a diagram that represents the solutions of a first order differential equation by arrows that are tangent to their graphs and that are oriented consistently with the "direction of propagation of the solutions". We can't draw such an arrow for every point of the #(x,y)#-plane (there are infinitely many points!), so we just approximate integral curves (i.e. graphs of the solutions) in some points of the plane. Depending on the regularity of #f(x,y)# we are able to guess how the solutions behave. This sentence is oversimplified, but the rigorous development requires a lot of theory, space and time. So take it as it is (and eventually ask below).
In our case #f(x,y)=x/4 (3-y)#. The "computational way" to draw the slope field is to do what a simple common plotting software would do: make the infinitesimal quantities not infinitesimal and turn the equation to #(Delta y) / (Delta x)=x/4 (3-y)#. Then substitute some values and plot the results of the computations.
This discretization process introduces error, so the smaller #Delta x# and #Delta y# the better.
Now we can choose a point #(x_0,y_0)# to start from, fix an arbitrary value #Delta x_0# of #Delta x# and evaluate #Delta y# for the point we chose, to get the corresponding value #Delta y_0#:
#Delta y=f(x,y) * Delta x => Delta y_0 =x_0/4 (3-y_0) * Delta x_0#
In our case, let's try fixing #Delta x_0=1# (I choose #1# to make calculations easier). We get #Delta y_0=x_0/4 (3-y_0)#. In this way we can draw an arrow starting from #(x_0,y_0)# and pointing to
#(x_0+Delta x_0,y_0 +Delta y_0)=(x_0+1,y_0+x_0/4(3-y_0))#.
The point #(x_0,y_0)# can be any point on the plane that is in the domain of #f(x,y)#. In our case, the domain is #mathbb{R}^2#, so let's choose "a few" points of the plane, do the calculations and plot the results:
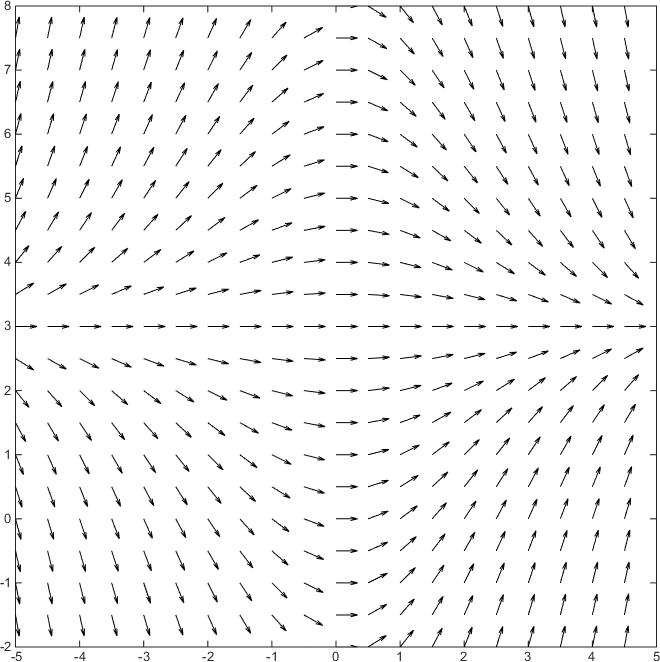
To make the graph look nicer, I drew same-length arrows.
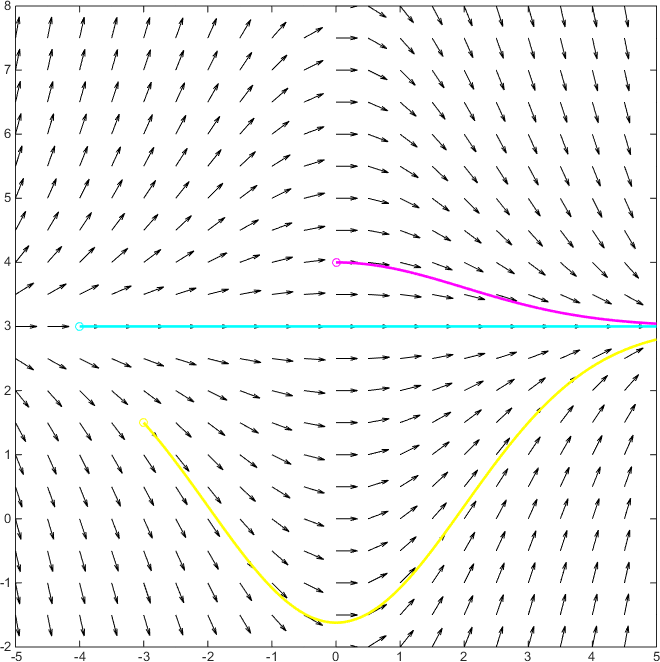
Now we can follow arrows to reconstruct solution's behavior. For example, if we start from point #(x_0,y_0)=(0,-4)# and we follow arrows, we get the magenta line of the graph below. Alternatively, if #(x_0,y_0)=(-4,3)# we get the cyan line and with #(x_0,y_0)=(-3,1.5)# the yellow one.
Notice that this equation is separable and the integral lines equations can be easily computed. This is an analytic alternative to the slope field plot, which gives exact results. In general, as you probably know, integration is not an easy task. So ours is a lucky situation.
Separating variables we get:
#1/(3-y) dy=x/4 dx#
Dividing by #3-y# implies that we have to exclude the line #y=3# from the possible solutions (otherwise #3-y# can be zero and we don't like null denominators). We have to test if it satisfies the differential equation, to check if we are removing some important stuff.
The derivative of this constant function is #dy/dx=0# and to compute #x/4(3-y)# we substitute #y=3# and get #0# for all real values of #x#. This means that #y=3# is actually a solution of the equation (both the derivative and #f(x,y)# are null) and has to be added to the solutions that we will find separating variables.
Now we can proceed with the integration. Let #k# be a real constant. Then:
#-ln|3-y| =x^2/8 + k#
#|3-y|=e^(-x^2/8-k)#
#3-y=pm e^(-x^2/8) e^{-k}#
#y=3 +C * e^(-x^2/8)#
where #C=-(pm e^{-k})# is a real constant such that #C ne 0# (in fact #e^(-k)>0#, so #pm e^{-k} ne 0#), introduced to simplify the expression. Notice that if we allow #C=0# too, we get #y=3#, This is the line that we excluded in order to be able to integrate.
Finally, we can express all the solutions with the following:
#y(x)=3+C * e^(-x^2/8)# for #C in mathbb{R}#
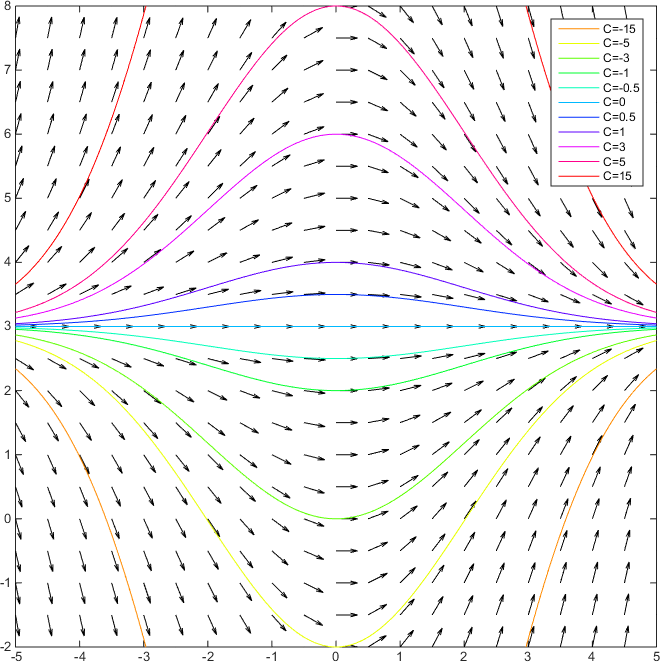
So if we plot #y(x)# for some values of #C#, we get the respective integral lines:
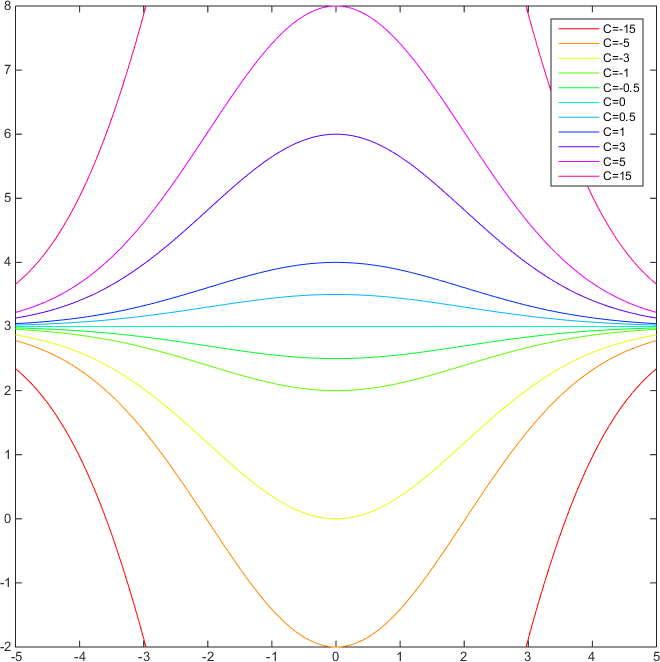
This shows that what we found drawing the slope field is consistent.
We can overlap the two diagrams to see this consistence: