Question

What is a slope field of a differential equation?

Answer 1

This is basically a graphical representation of many derivatives of one function, including vertical shifts, illustrating how the solution to an indefinite integral involves all vertical shifts, "`+C`"

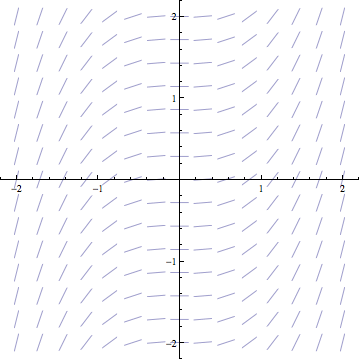
A slope field is a way of describing the function `f(x) + C` by tracing its derivative at multiple points within a viewing window, including all of its vertical shifts.

When you see a slope field like this, if you simply connect the dashes together and make a curve, you trace the curve itself at some `+C` shift. Each dash corresponds to a single derivative at some value of `x`.