How do you evaluate an integral with an absolute value? Question below.
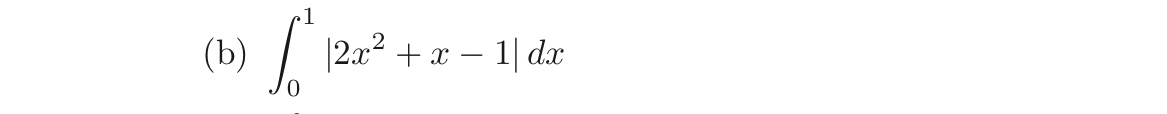
1 Answer
Dec 9, 2017
Explanation:
Once I found roots of integrand,
Hence
Integrand was negative when
Consequently,
=
=
=
=
=
=
=
=
=
Thus,
=
=
=

