How do you evaluate #cos((2pi)/3)#?
1 Answer
Apr 25, 2016
Explanation:
The angle
# (2pi)/3" is in the 2nd quadrant "#
where the cos ratio has a negative value.The related 'acute angle' to
#(2pi)/3 =( pi -(2pi)/3) = pi/3 #
#rArr cos((2pi)/3) = - cos(pi/3) # and using the
#color(blue)" Exact value triangle"#
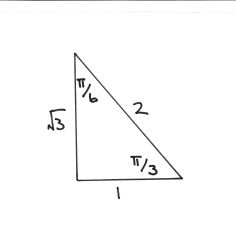
# cos((2pi)/3) = - cos(pi/3) = -1/2 #
