Question

How do you evaluate `Sin (165)`?

Answer 1

`sin 165^@ = 1/4(sqrt(6)-sqrt(2))`

Explanation:

Some things we will use:

`sin(theta) = sin (180^@ - theta)`

`sin(alpha-beta) = sin alpha cos beta - sin beta cos alpha`

`sin 45^@ = cos 45^@ = sqrt(2)/2`

`sin 30^@ = 1/2`

`cos 30^@ = sqrt(3)/2`

Hence we find:

`sin 165^@ = sin (180^@-165^@)`

`color(white)(sin 165^@) = sin 15^@`

`color(white)(sin 165^@) = sin (45^@ - 30^@)`

`color(white)(sin 165^@) = sin 45^@ cos 30^@ - sin 30^@ cos 45^@`

`color(white)(sin 165^@) = sqrt(2)/2 sqrt(3)/2 - 1/2 sqrt(2)/2`

`color(white)(sin 165^@) = 1/4(sqrt(6)-sqrt(2))`

`color(white)()`
Footnotes

The trigonometric values we used in our derivation can be observed in the following right angled triangles:

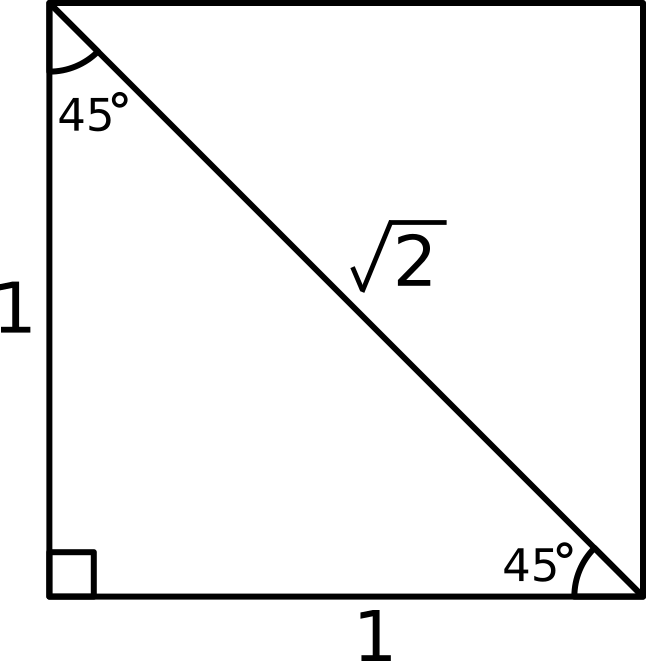
Hence `sin 45^@ = cos 45^@ = 1/sqrt(2) = sqrt(2)/2`

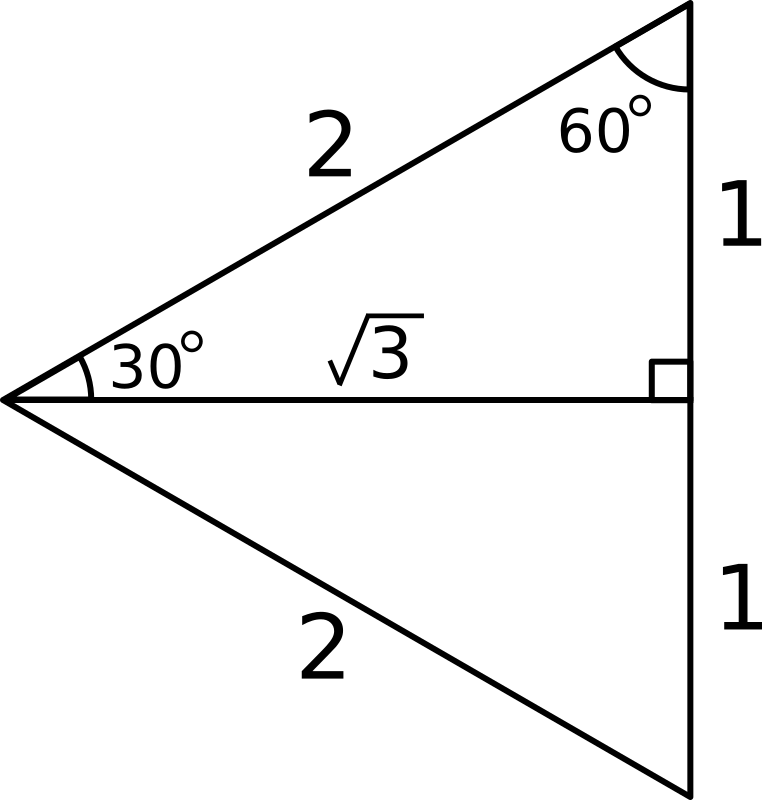
Hence `sin 30^@ = 1/2` and `cos 30^@ = sqrt(3)/2`